Super Machine Learning Revision Notes
Contact me
- Blog -> https://cugtyt.github.io/blog/index
- Email -> cugtyt@qq.com
- GitHub -> Cugtyt@GitHub
本系列博客主页及相关见此处
来自Super Machine Learning Revision Notes,重点参考An overview of gradient descent optimization algorithms
Activation Functions
| Name | Function | Derivative |
|---|---|---|
| sigmoid | $\sigma(z)=\frac{1}{1+e^{-z}}$ | $g(z)(1-g(z))$ |
| tanh | $tanh(z) =2 \sigma(2z) - 1 = \frac{e^z - e^{-z}}{e^z + e^{-z}}$ | $1-(tanh(z))^2$ |
| Relu | $\max (0, z)$ | $0, if \ z<0 \ 1, if \ z > 0, \ undefined, if \ z =0$ |
| Leaky Relu | $\max (0.01z, z)$ | $0.01, if \ z<0 \ 1, if \ z > 0, \ undefined, if \ z =0$ |
梯度下降
GD:
\[\theta = \theta - \eta \cdot \nabla_\theta J(\theta)\]SGD:
\[\theta = \theta - \eta \cdot \nabla_\theta J(\theta:x^{(i)};y^{(i)})\]Mini-batch GD:
\[\theta = \theta - \eta \cdot \nabla_\theta J(\theta:x^{(i:i+n)};y^{(i:i+n)})\]Momentum:
\[v_t = \gamma v_{t-1} + \eta \cdot \nabla_\theta J(\theta) \\ \theta = \theta - v_{t}\]$\gamma$通常取0.9或差不多的值。
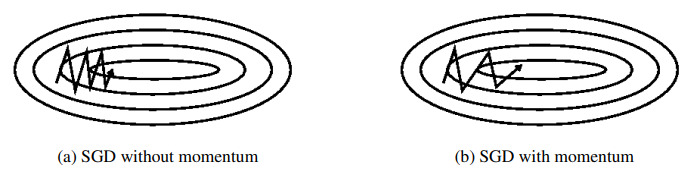
Nesterov:
向前看一步动量
\[v_t = \gamma v_{t-1} + \eta \cdot \nabla_\theta J(\theta - \gamma v_{t-1}) \\ \theta = \theta - v_{t}\]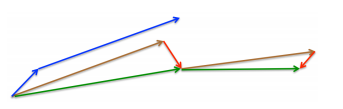
RMSprop
\[E[g^2]_t = 0.9 E[g^2]_{t-1} + 0.1 g_t^2\\ \theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_t\]Adam
第二步修正是为了解决学习率太小,导致偏向0,因为$\beta$取值接近1。相当于Adadelta和RMSProp加入动量(一阶)。
\[m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t\\ v_t = \beta_2 v_{t-1} + (1 - \beta_2)g_t^2\\ \hat{m_t} = \frac{m_t}{1-\beta_1^t}\\ \hat{v_t} = \frac{v_t}{1-\beta_2^t}\\ \theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}\hat{m_t}\]BN
\[\mu = \frac{1}{m} \sum Z^{(i)}\\ \sigma^2 = \frac{1}{m} \sum(z^{(i)} - \mu) \\ Z_{normalized}^{(i)} = \alpha \frac{Z^{(i) - \mu}}{\sqrt{\sigma^2}+\epsilon} + \beta\]初始化
Xavier
Xavier初始化的基本思想是,若对于一层网络的输出和输出可以保持正态分布且方差相近,这样就可以避免输出趋向于0,从而避免梯度弥散情况。
对于$y=wx$,根据假设有:
\[Var(Y) \\= Var(w_i X) \\= Var(w_i) * Var(X) + E^2(X)Var(w_i) + E^2(w_i) Var(X)\]当$X,w_i$符合均值0的正太分布时,期望$E(X),E(w_i)$均为0,上式可化简:
\[Var(Y) = Var(w_i) * Var(X)\]如果有$n_i$个神经元,那么
\[Var(Y) = n_i * Var(w_i) * Var(X)\]要$Var(Y) = Var(X)$,则需要$n_i * Var(w_i)=1$,即$Var(w_i) = 1/n_i$,同理反向传播时:$Var(w_i) = 1/n_{i+1}$,因此:
$Var(w_i) = 2/(n_i+n_{i+1})$
因此正态分布可以为$N(0, 2/(n_i+n_{i+1}))$
对于均匀分布$X\sim U(a,b)$有:
\[E = (a+b)/2=0\\ Var = (b-a)^2/12 = 2/(n_i + n_{i+1})\]得:
\[a = -b = -\sqrt{6/(n_i + n_{i+1})}\]He
在ReLU网络中,假定每一层有一半的神经元被激活,另一半为0,所以要保持方差不变,只需要在 Xavier 的基础上再除以2
\[Var(w_i) = 2/n_i\]