OpenAI Spinning Up Part 1： Key Concepts in RL

Contact me

• Blog -> https://cugtyt.github.io/blog/index
• Email -> cugtyt@qq.com
• GitHub -> Cugtyt@GitHub

---

来自OpenAI Spinning Up Introduction to RL

简而言之，RL是研究agent(智能体，本文保留英文描述)如何通过反复的尝试来学习。我们通过奖励或惩罚agent的行为，使其在未来能以更高的概率去重复或放弃该行为。

Key Concepts and Terminology

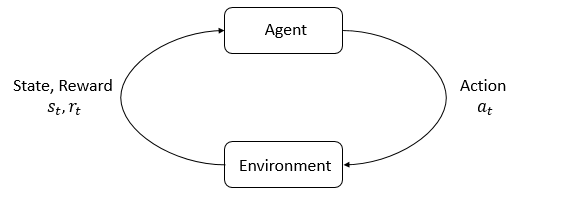
RL的主要特征是agent和环境。环境是agent居住并与之互动的世界。在每一次互动中，agent都会对世界有一个(可能是部分的)观察，然后决定要采取的行动。环境会随着agent的互动发生变化，也可能环境会自行更改。

agent会感知来自环境的奖励信号，这个数字告诉它当前世界状态的好坏。agent的目标是最大化其累积奖励，称为回报，RL就是让agent学习更好的行为以实现这个目标。

为了更具体地讨论RL做什么，我们需要引入一些术语：

• 状态和观察(states and observations)
• 行为空间(action spaces)，
• 策略(policies)，
• 轨迹(trajectories)，
• 不同的回报方式(different formulations of return)，
• RL优化问题(the RL optimization problem)，
• 值函数(value functions)。

States and Observations

状态(states)是对世界状况的完整描述，没有隐藏信息。观察(observations)是对状态的部分描述，有一些信息被略掉了。

在深度RL中，我们几乎总是通过实值向量，矩阵或高阶张量来表示状态和观察。例如，视觉观察可以由其RGB像素矩阵表示，机器人的状态可以用它的关节角度和速度来表示。

当agent能够观察到环境的完整状态时，我们说环境被完全观察(fully observed)，当agent只能看到部分环境时，我们说环境被部分观察(partially observed)。

强化学习符号通常把状态表示为$s$，但是表示观察$o$更合适。通常这用于讨论agent去决定采取一个行为：我们通常说动作是以状态为条件的，但是实际上，动作是以观察为条件的，因为agent没有接触到状态。

在这里，我们将遵循标准约定，但应从上下文中可以明确区分。

(这里有点绕，说白了就是agent只能观察环境，不能直接得到环境的状态)

Action Spaces

不同的环境允许不同类型的行为，给定环境中的所有有效行为集合通常称为行为空间。某些环境(如Atari和Go)具有离散的行为空间，agent只有有限数量可采取的行为。其他环境中例如agent控制物理世界中的机器人，具有连续的行为空间，在连续空间中，行为是实值向量。

这个区别对深度RL中的方法有非常深刻的影响。一些算法族只能在某种情况下应用，而对于其他情况则必须重做。

Policies

策略是agent用来决定行为的规则。它可以是确定性的，在这种情况下通常表示为$\mu$：

\[a_t = \mu(s_t),\]

或者是随机的，表示为$\pi$：

\[a_t \sim \pi(\cdot \vert s_t).\]

策略本质上是agent的大脑，因此将“策略”一词替换为“agent”也比较常见，例如可以说“策略试图最大化奖励”。

在深度RL中，我们使用的是参数化策略：策略的输出是可计算的函数，函数依赖于一组参数(就像神经网络的权重和偏差)，我们可以通过某种优化算法来调整函数进而改变行为。

我们经常用$\theta$或$\phi$表示这种策略的参数，将其写在策略符号下标：

\[a_t = \mu_{\theta}(s_t) \\ a_t \sim \pi_{\theta}(\cdot \vert s_t).\]

Deterministic Policies

确定性策略示例。用Tensorflow在连续行为空间构建简单的确定性策略代码：

obs = tf.placeholder(shape=(None, obs_dim), dtype=tf.float32)
net = mlp(obs, hidden_dims=(64,64), activation=tf.tanh)
actions = tf.layers.dense(net, units=act_dim, activation=None)

其中mlp是一个函数，是用多个dense层堆叠在一起表示的。

Stochastic Policies

深度RL中两种最常见的随机策略是类别策略(Categorical Policies)和对角高斯策略(Diagonal Gaussian Policies)。类别策略可用于离散行为空间，而对角高斯策略用于连续行为空间。使用和训练随机策略有两个关键计算：

• 从策略中采样行为(sampling actions from the policy)
• 计算特定行为的log似然函数$\log \pi_\theta (a \vert s)$(computing log likelihoods of particular actions)

Categorical Policies 类别策略就像离散动作的分类器。分类策略构建神经网络的方式与分类器相同：输入是观察，然后是一些层(可能是卷积或全连接，取决于输入的类型)，最后是线性层，提供每个行为的logits，接着是softmax，将logits转换为概率。

Sampling 基于每个行为的概率，Tensorflow等框架有内置的采样工具来采样。例如tf.distributions.Categorical文档或tf.multinomial。

Log-Likelihood。将最后一层概率表示为$P _ {\ theta}(s)$。它是一个向量，我们可以将行为视为向量的索引，然后通过向量索引来获取动作$a$的对数似然： \(\log \pi_{\theta}(a \vert s) = \log \left[P_{\theta}(s)\right]_a.\)

Diagonal Gaussian Policies 多元高斯分布(或多元正态分布)由平均向量$μ$和协方差矩阵$\Sigma$来描述。对角高斯分布是一种特殊情况，其中协方差矩阵仅在对角线上具有值，因此我们可以用向量表示它。

对角高斯策略总是用一个神经网络将观察映射到动作均值，$\mu _ {\theta}(s)$。通常有两种不同的表示协方差矩阵的方式。

第一种方式：用一个对数标准差向量，$\log \sigma$，它不是状态函数，是独立参数。 (VPG，TRPO和PPO的实现方式是这样做的)

第二种方式：用神经网络将状态映射到对数标准差，$\log \sigma _ {\theta}(s)$。它可以选择与均值网络共享一些层。

注意，在这两种情况下，我们都直接输出对数标准差而不是标准差。这是因为对数标准差可以容易的取到$(- \infty，\infty)$中的任何值，而标准差必须是非负的，没有这些约束会更容易训练参数。标准差可以通过对对数标准差取幂获得，所以这种表示没有任何损失。

Sampling 给定动作均值$\mu _ {\theta}(s)$和标准差$\sigma _ {\theta}(s)$，以及来自球形高斯的噪声向量z($z \sim \mathcal {N}(0,I)$ )，行为采样可以用如下计算获得： \(a = \mu_{\theta}(s) + \sigma_{\theta}(s) \odot z\) 其中$\odot$表示两个向量的元素乘积。框架都具有计算噪声向量的内置方法，例如tf.random_normal。

Log-Likelihood 对于具有均值$\mu = \mu _ {\theta}(s)$和标准差$\sigma = \sigma _ {\theta}(s)$的对角高斯分布，k维行为a的对数似然性由下式给出： \(\log \pi_{\theta}(a \vert s) = -\frac{1}{2}\left(\sum_{i=1}^k \left(\frac{(a_i - \mu_i)^2}{\sigma_i^2} + 2 \log \sigma_i \right) + k \log 2\pi \right).\)

Trajectories

轨迹$\tau$是在世界中的一系列状态和行为，

\[\tau = (s_0, a_0, s_1, a_1, ...).\]

世界的第一个状态$s_0$是从起始状态分布中随机抽样的，有时用$\rho_0$表示：

\[s_0 \sim \rho_0(\cdot).\]

状态转换(在时间t的状态$s_t$和t+1的状态$s_ {t + 1}$之间发生的事情)受环境的自然规律支配，并且仅依赖于最近的行为$a_t$。它们可以是确定性的:

\[s_{t+1} = f(s_t, a_t)\]

也可以是随机的：

\[s_{t+1} \sim P(\cdot \vert s_t, a_t).\]

行动由agent根据其策略采取。

trajectories也经常被称为episodes或rollouts。

Reward and Return

奖励函数R在强化学习中至关重要。它取决于当前的世界状态，采取的行动以及世界的下一个状态：

\[r_t = R(s_t, a_t, s_{t+1})\]

虽然经常将其简化为仅依赖于当前状态$r_t = R(s_t)$或状态-行为$r_t = R(s_t，a_t)$。

agent的目标是在轨迹上最大化累积奖励，我们将用$R(\tau)$来表示所有的奖励。

一种回报是有限期未折现的回报(finite-horizon undiscounted return)，它就是在固定的步骤窗口中获得的奖励总和：

\[R(\tau) = \sum_{t=0}^T r_t.\]

另一种回报是无限期折现回报(infinite-horizon discounted return)，它是agent获得的所有奖励的总和，但是对获得奖励的距离进行折现。这种奖励形式有一个折现因子$\gamma \in(0,1)$：

\[R(\tau) = \sum_{t=0}^{\infty} \gamma^t r_t.\]

为什么要一个折现因子呢？不是要获得所有奖励吗？虽然如此，但折现因子不仅直观而且在数学也方便。在直观的层面上：当前的奖励比后续的更好。数学上：无限期的奖励总和可能不会收敛到有限值，并且很难在方程中处理，但是在折现因子以及一定的条件下，这个求和是收敛的。

虽然这两种回报方式之间的界限非常明显，但这个界限在深度RL实践中往往没那么清晰，例如我们经常会设置算法去优化未折现的回报，但在估算值函数时却又使用折现因子。

The RL Problem

无论回报方式选什么(无限期折现，还是有限期未折现)，无论策略的选择如何，RL的目标都是选择一种策略，当agent根据它采取行动时能最大化预期回报。

谈到预期回报，我们首先要讨论轨迹上的概率分布。

我们假设环境转换和策略都是随机的。 在这种情况下，T步轨迹的概率为：

\[P(\tau \vert \pi) = \rho_0 (s_0) \prod_{t=0}^{T-1} P(s_{t+1} \vert s_t, a_t) \pi(a_t \vert s_t).\]

由$J(\pi)$表示预期收益为：

\[J ( \pi ) = \int _ { \tau } P ( \tau \vert \pi ) R ( \tau ) = \underset { \tau \sim \pi } { \mathrm { E } } [ R ( \tau ) ]\]

RL中的核心优化问题可以表示为：

\[\pi^* = \arg \max_{\pi} J(\pi),\]

其中$\pi ^ *$是最优策略。

Value Functions

了解状态或状态-动作对的值通常很有用。值指的是从该状态或状态-行动对开始的预期回报，然后一直根据特定策略行事。几乎每种RL算法都以这样或那样的方式在使用值函数。

这里有四个主要函数：

• On-Policy Value Function，$V ^ {\pi}(s)$，从状态s开始并且总是根据策略$\pi$执行行为，它会给出预期的回报为：

  \[V^{\pi}(s) = \underset {\tau \sim \pi}E [R(\tau)\left\vert s_0 = s \right]\]

• On-Policy Action-Value Function，$Q ^ {\ pi}(s，a)$，从状态s开始，采取任意行动a(可能不是来自策略),总是根据策略$\pi$执行行为,它给出预期的回报：

  \[Q^{\pi}(s,a) = \underset {\tau \sim \pi}E[R(\tau)\left\vert s_0 = s, a_0 = a\right.]\]

• Optimal Value Function, $V ^ (s)$，从状态s开始并且始终根据环境中的最优*策略执行，则给出预期的回报：

  \[V^*(s) = \max_{\pi} \underset {\tau \sim \pi}E[R(\tau)\left\vert s_0 = s\right.]\]

• Optimal Action-Value Function，$Q ^ (s，a)$，从状态s开始，采取任意动作a，然后根据环境中的最优*策略采取行动，给出预期回报：

  \[Q^*(s,a) = \max_{\pi} \underset{\tau \sim \pi}E[R(\tau)\left\vert s_0 = s, a_0 = a\right.]\]

在谈论价值函数时，如果不考虑时间依赖性，那就只是在表示无限期折现回报的期望均值。有限期无折现回报的值函数需要有时间作为参数。

值函数和动作-值函数之间有两个关键的联系经常出现： \(V^{\pi}(s) = \underset {a\sim \pi}E[Q^{\pi}(s,a)],\) \(V^*(s) = \max_a Q^* (s,a).\) 这些关系直接来自刚刚给出的定义：你能证明它们吗？

The Optimal Q-Function and the Optimal Action

最优动作-值函数$Q ^ *(s，a)$与最优策略选择的动作之间存在重要联系。根据定义，$Q ^ *(s，a)$给出了在状态s中开始,采取(任意)动作a，然后一直根据最优策略行动的预期回报。

s中的最优策略将选择从s开始最大化预期回报的行为。因此如果我们有$Q ^ *$，我们可以通过这个式子直接获得最优动作$a ^ *(s)$：

\[a^*(s) = \arg \max_a Q^* (s,a).\]

注意：可能存在多个最大化$Q ^ *(s，a)$的行为，在这种情况下，所有动作都是最优的，最优策略可以随机选择它们中的任何一个，但总存在一种确定性选择行为的最优策略。

Bellman Equations

所有的四个值函数都遵循称为Bellman方程的特殊自洽方程。Bellman方程背后的基本思想是：

起始点的值是从当前位置获得的奖励期望，在加上下次落脚点值的期望。(The value of your starting point is the reward you expect to get from being there, plus the value of wherever you land next.)

On-Policy Value Function的Bellman方程是

\[V^{\pi}(s) = \underset {a \sim \pi \\ s'\sim P}E[r(s,a) + \gamma V^{\pi}(s')], \\ Q^{\pi}(s,a) = \underset{s'\sim P}E[r(s,a) + \gamma \underset{a'\sim \pi}E[Q^{\pi}(s',a')],\]

其中$s’\sim P$是$s’\sim P(\cdot \vert s，a)$的简写，表示从环境转换规则中采样的下一个状态$s’$; $a \sim \pi$是$\sim \pi(\cdot \vert s)$的简写; 而$a’\sim \pi$是$a’\sim \pi(\cdot \vert s’)$的简写。

Optimal Value Function的Bellman方程是

\[V^*(s) = \max_a \underset{s'\sim P}E[r(s,a) + \gamma V^*(s')], \\ Q^*(s,a) = \underset {s'\sim P}E[r(s,a) + \gamma \max_{a'} Q^*(s',a')].\]

On-Policy Value Function与Optimal Value Function的Bellman方程之间的关键区别在于在行为上有没有取$\max$,它的意思是，为了达到最优的目标，agent必须选择那个具有最高值的行为。

Advantage Functions

在RL中，我们不去描述行为绝对好多少，而只需要说它比其它行为平均好多少。也就是说，我们想知道该行为的相对优势，优势函数将精确描述这个概念。

对于策略$\pi$的优势函数$A ^ {\pi}(s，a)$描述了在状态s中采取特定动作a比根据$\pi(\cdot \vert s)$随机选择动作要好多少,这里假设一直按照$\pi$采取行动。在数学上优势函数定义为：

\[A^{\pi}(s,a) = Q^{\pi}(s,a) - V^{\pi}(s).\]

我们稍后会对此进行讨论，但优势函数对于策略梯度方法至关重要。

(Optional) Formalism

到目前为止，我们已经以非正式的方式讨论了agent的环境，但是如果深入研究文献，你很可能会遇到一个标准数学形式：马尔可夫决策过程(MDP)。 MDP是一个5元组，$\langle S，A，R，P，\rho_0 \rangle$，其中

• $S$ is the set of all valid states,
• $A$ is the set of all valid actions,
• $R$ : $S \times A \times S \to \mathbb{R}$ is the reward function, with $r_t = R(s_t, a_t, s_{t+1})$,
• $P$ : $S \times A \to \mathcal{P}(S)$ is the transition probability function, with $P(s’\vert s,a)$ being the probability of transitioning into state s’ if you start in state s and take action a,
• and $\rho_0$ is the starting state distribution.

马尔可夫决策过程这个名称指的是系统服从马尔可夫属性：状态转换只取决于最近的状态和行动，而不是先前的历史。