A Review on Generative Adversarial Networks: Algorithms, Theory, and Applications
Contact me
- Blog -> https://cugtyt.github.io/blog/index
- Email -> cugtyt@qq.com
- GitHub -> Cugtyt@GitHub
本系列博客主页及相关见此处
3 算法
3.1 GAN
3.1.1 Objective function
\[\min_G \max_G V(D, G) = E_{x \sim p_{data}} [\log D(x)] + E_{z \sim p_z} [\log(1 - D(G(z)))]\]固定G,最优的D为
\[D^*_G(x) = \frac{p_{data}}{p_{data} + p_g}\]最小最大博弈就可以写成:
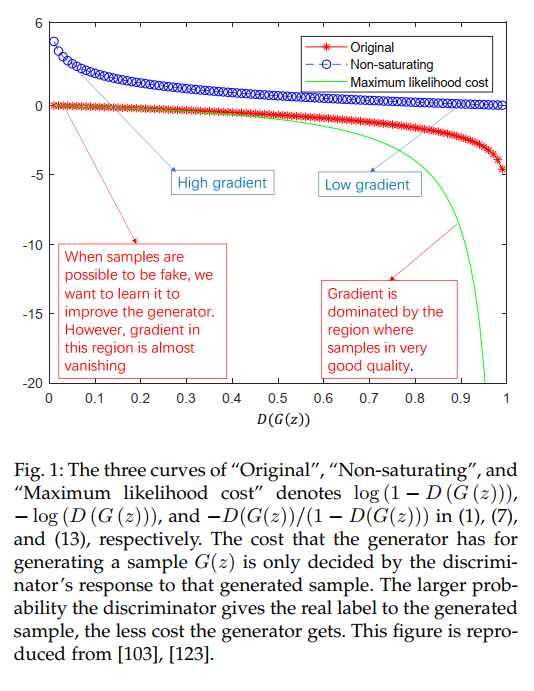
\[\max_D V(D, G) = \\ E_{x \sim p_{data}} [\log \frac{p_{data}}{p_{data} + p_g}] + E_{x \sim g} \frac{p_{data}}{p_{data} + p_g} - 2 \log 2\\ = 2 JS(p_{data} \Vert p_g) - 2 \log 2\]在训练早期,G很差,D很容易判别,因此$\log (1 - D(G(z)))$就饱和了,这时候可以最大化$\log D(G(z))$。这样提供了更大的梯度。
下图展示了三种GAN目标的图像:
3.2 GANs’ representative variants
3.2.1 InfoGAN
不光是用噪声作为输入,还加入了信息编码
\[\min_G \max_D V_I (D, G) = V(D, G) - \lambda I(c; G(z, c))\]但是第二项需要获取到后验概率$P(c\vert x)$因此不好直接优化,因此使用一个近似分布$Q(c\vert x)$表示$P(c\vert x)$的下界。
3.2.2 cGAN
给定额外信息的情况下可以构建条件GAN:
\[\min_G \max_D V(D, G) = E_{x \sim p_{data}} [\log D(x \vert y)] + E_{z\sim p_{z}} [\log (1 - D(G(z \vert y)))]\]和infoGAN相似,但是infoGAN的隐码是不知道的需要学习。infoGAN需要额外的网络学习$Q(c\vert x)$

3.2.3 CycleGAN
如果不存在合适的样本对的话没法直接训练判别器,CycleGAN可以通过反向再次生成解决这个问题。