LARGE BATCH TRAINING OF CONVOLUTIONAL NET NETWORKS
Contact me
- Blog -> https://cugtyt.github.io/blog/index
- Email -> cugtyt@qq.com
- GitHub -> Cugtyt@GitHub
本系列博客主页及相关见此处
ABSTRACT
通常加速训练卷积网络的方法是增加计算单元,使用数据并行的SGD,把批量数据分发到计算单元上,随着计算节点的增加,批量也增大。但是使用大批量会导致很低的模型准确率。我们认为当前对大批量训练的处理(线性学习率放大,以及warm-up)不能够很好的泛化,训练会发散。为了克服优化的困难,我们提出了基于层的自适应学习率方法Layer-wise Adaptive Rate Scaling (LARS)。通过这个方法,我们把Alexnet的批量放大到了8K,Resnet-50的批量放大到32K,同时没有准确率损失。
1 INTRODUCTION
通常使用更多的计算资源,增大批量来加快训练,但是增大批量通常会导致准确率降低。保持训练轮数,增大批量,意味着更新权重的次数变少。直接的方法是同比例放大学习率。但是使用大的学习率让优化更加困难,网络可能在初始阶段就发散了。为了解决这个困难,有人提出了学习率warm-up,从一个小的学习率开始,缓慢增加到我们需要的学习率。通过warm-up和线性放大,成功的将Resnet50用8K的批量训练。这也是当前最好的训练大批量策略。
我们尝试将这种方法在ImageNet上训练AlexNet,但是在2K批量的时候就开始发散了。对于4K的批量,准确率从57.6(256批量)到53.1,8K批量的时候准确率降到44.8%。为了使用大学习率,我们把局部响应标准化层 Local Response Normalization替换为Batch Normalization (BN),记作AlexNet-BN。BN帮助了收敛,提高了准确率,对于8K的批量,准确率的差距从14%降低到了2.2%。
为了分析大学习率的训练稳定性,我们测量了层权重范数和梯度范数norm的比值。观察到,如果这个比值太大,训练就会不稳定,另外,如果比值太小,权重更新不够快。这个比值在不同的层情况不同,因此对不同的层使用不同的学习率是必要的。因此我们提出了Layer-wise Adaptive Rate Scaling (LARS),LARS和自适应学习算法例如ADAM或RMSProp不同之处在于:首先,LARS对不同的层而不是不同的权重使用不同的学习率,其次,更新的量由权重的范数控制,用于更好的控制训练速度。使用LARS训练Alexnet-BN和Resnet50,批量可以达到32K也没有准确率损失。
2 BACKGROUND
通常使用随机梯度SG训练CNN,每一步t,采样一个批量B的样本$x_i$,计算损失函数梯度$\nabla L(x_i, w)$,更新网络权重:
Krizhevsky建议使用如下方法训练大批量:批量B增大k倍,增大学习率k倍,其他超参数不动。例如$k=2$的时候,权重更新两轮为:
\[w_{t+2}=w_{t}-\lambda * \frac{1}{B}\left(\sum_{i=1}^{B} \nabla L\left(x_{i}, w_{t}\right)+\sum_{j=1}^{B} \nabla L\left(x_{j}, w_{t+1}\right)\right.\]批量为2倍$B_2=2*B$的时候,学习率$\lambda_2$,权重更新为:
假设$\nabla L\left(x_{j}, w_{t+1}\right) \approx L(x_j, w_t)$,带入$\lambda_2=2*\lambda$,二者就很相近了。
使用线性学习率放大,批量1K会有很小的准确率损失。批量2K就困难了,训练开始发散。使用BN会好很多。
另外有人结合了学习率warm-up,他们是当前最好的训练大批量的方法。
此外,有观察到大批量的泛化性会降低,得出的结论是大批量会收敛到尖锐的局部最优,但是没有解决方法。
3 ANALYSIS OF ALEXNET TRAINING WITH LARGE BATCH
使用BVLC实现的Alexnet,批量512作为基线。使用SGD,动量0.9,初始学习率0.01,2次多项式衰减100轮。基线准确率58%。然后,我们使用大学习率,批量4K,学习率调到0.08,但是学习率大于0.06后,即使是用warm-up也会发散。最后的准确率是批量4K下得到53.1%,学习率0.05。见表1(a)。
为了稳定训练,我们把Local Response Normalization换成了BN层,批量512的基线为60.2%,使用BN可以不用warm-up的情况下使用大的学习率,批量4K,最好的准确率是58.9%(学习率0.18),批量8K准确率58%(学习率0.3)。
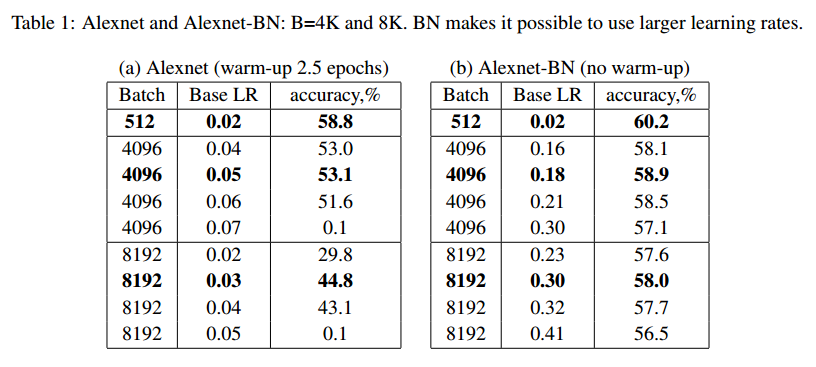
在批量8K的时候仍然有2.2%准确率的损失。我们观察了训练和测试曲线,没有发现显著的差异。我们的结论是准确率下降不是因为泛化差异,二十训练不足。
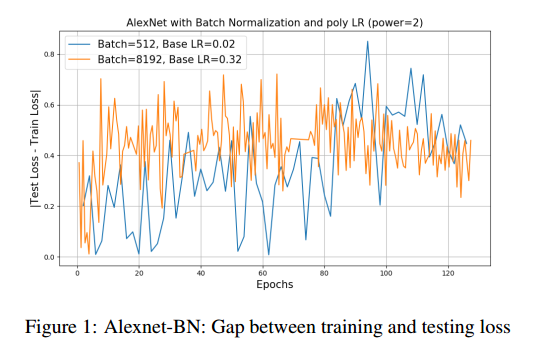
4 LAYER-WISE ADAPTIVE RATE SCALING (LARS)
标准的SGD对所有层使用同样的学习率,$w_{t+1}=w_t-\lambda \nabla L(w_t)$。学习率很大的时候,更新$\Vert \lambda * \nabla L(w_t) \Vert$可能比$\Vert w \Vert$大,这会导致发散。这让初始阶段的对初始权重和初始学习率高度敏感。我们发现权重和梯度的L2范数比值$\Vert w \Vert / \Vert \nabla L(w_t)\Vert$在权重和偏置上,以及层之间差异很大,如表2。比值在初始阶段很大,几轮之后减小。
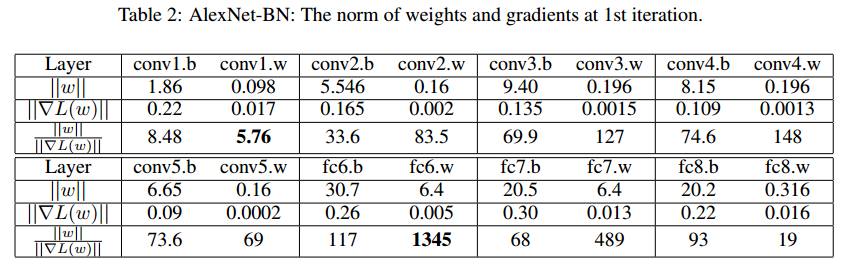
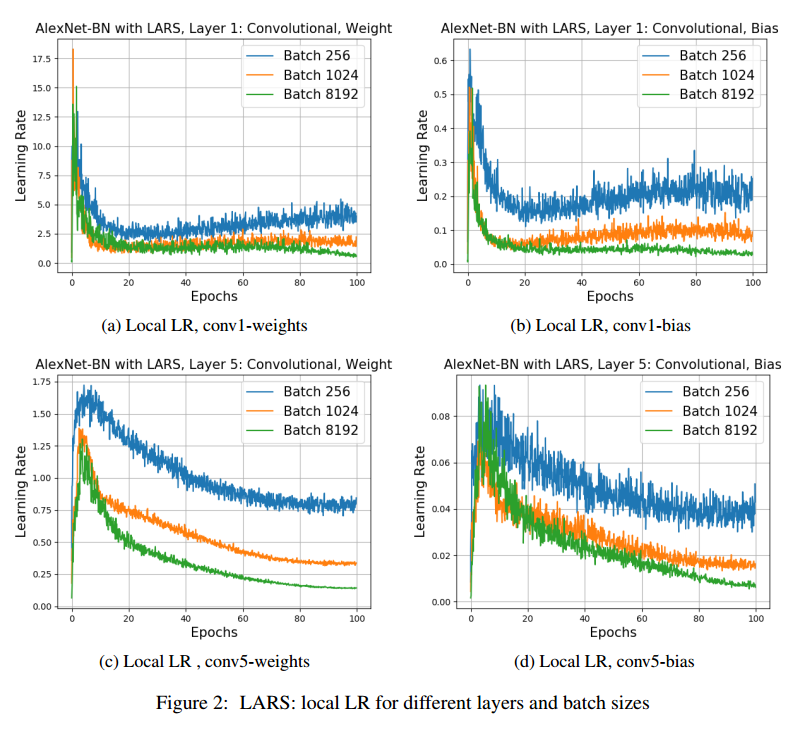
对于某些层,如果学习率大于这个比值,训练就开始不稳定了。学习率warm-up可以来解决这个问题。
我们希望使用不同的方法,对每层$l$使用局部学习率$\lambda ^l$:
\[\Delta w_t^l = \gamma * \lambda ^l * \nabla L(w_t^l)\]其中$\gamma$是全局学习率,局部学习率通过置信相关度$\eta <1$来定义:
\[\lambda ^l = \eta \times \frac{\Vert w^l \Vert}{\Vert \nabla L(w_t)\Vert}\]注意,现在更新的量不在取决于梯度的大小,因此可以部分减少梯度消失和爆炸的问题。可以容易的进行扩展,平衡学习率和权重衰减项$\beta$:
\[\lambda ^l = \eta \times \frac{\Vert w^l \Vert}{\Vert \nabla L(w_t)\Vert + \beta * \Vert w^l \Vert}\]
5 TRAINING WITH LARS
使用批量32K,再次训练Alexnet和Alexnet-BN,如图3,【略】
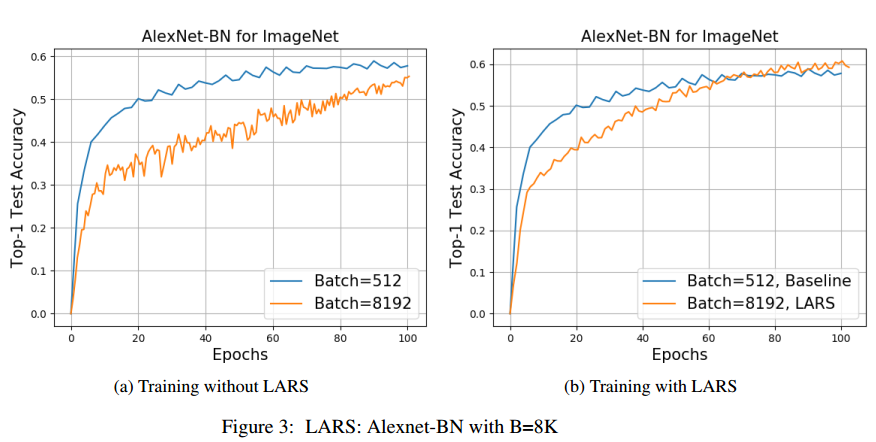
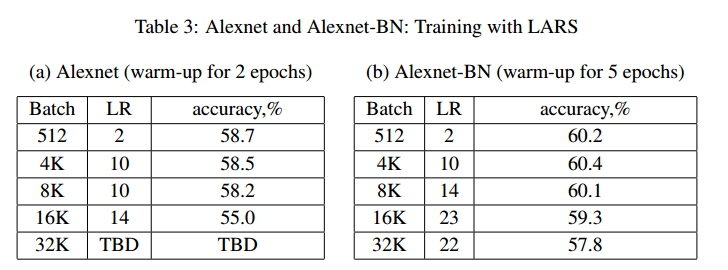
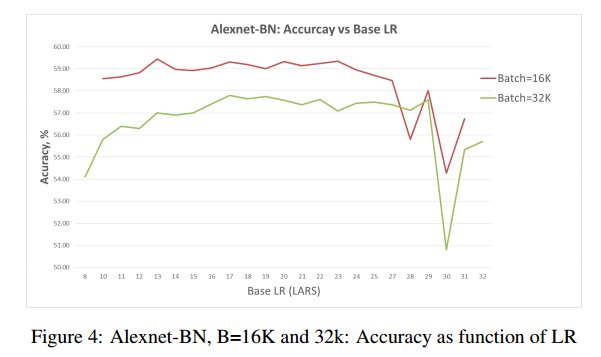
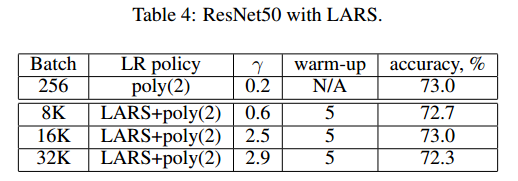
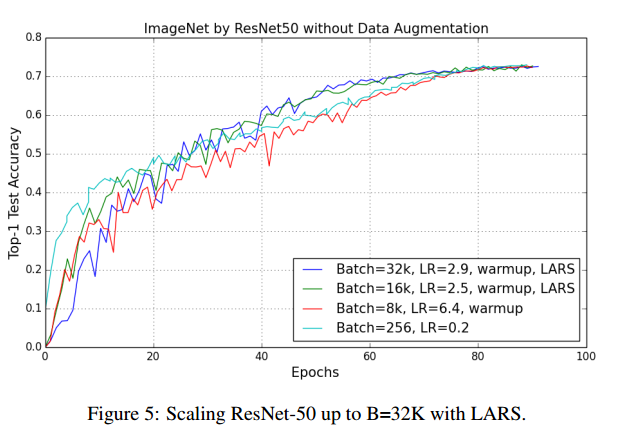
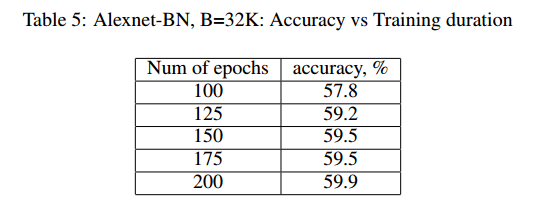
7 CONCLUSION
提出了LARS,可以使用32K的批量训练Alexnet和Resnet50,高于32K批量如何不损失准确率仍然是个问题。