A New Backpropagation Algorithm withoutGradient Descent
Contact me
- Blog -> https://cugtyt.github.io/blog/index
- Email -> cugtyt@qq.com
- GitHub -> Cugtyt@GitHub
本系列博客主页及相关见此处
Abstract
反向传播算法最初在20世纪70年代引入,是神经网络学习的主力。反向传播算法使用的是梯度下降方法,是一种一阶迭代优化算法。梯度下降为了找到函数的局部最小值,沿着反向梯度的方法进行寻找。在本文中,我们开发了一种不使用梯度下降算法的反向传播替代方法,使用Moore-Penrose伪逆寻找神经元的权重和偏置误差。
1 Introduction
梯度下降通过不断迭代逼近局部最小值。它基于一个观察,即如果多元函数$F(x)$在点$a$的邻域有定义且可微,那么$F(x)$在$a$点梯度反方向$-\Delta F(a)$就是下降最快的方向。那么如果$a_{n+1}=a_{n}-\gamma \Delta F\left(a_{n}\right)$,在$\gamma$足够小时,有$F\left(a_{n}\right)>=F\left(a_{n+1}\right)$。
即使这个方法通常工作得不错,但是有一些局限。第一,由于算法的迭代特性,收敛耗时。第二,在最小值附近下降很慢。第三,不适用于不可微函数。
Moore-Penrose伪逆,在数学上尤其是线性代数上,矩阵$\mathrm{A}$的伪逆$\mathrm{A}+$是逆矩阵的泛化。通常使用伪逆来计算非唯一解的线性等式的最优拟合(best fit)。另一个用途是多解等式的最小欧几里得norm解。
2 Modifications to the neuron structure
我们对神经元做了一个结构上的改变。我们假设每个输入有一个权重和偏置。和传统神经元的区别是传统的偏置是加在网络的输出上的。这个改变不会影响网络的结果和目标。证明如下:
对于大小为n的输入向量:
\(c_{1} w_{1}+b_{1}+c_{2} w_{2}+b_{2}+c_{3} w_{3}+b 3 \ldots c_{n} w_{n}+b_{n} \qquad (1)\) \(=c_{1} w_{1}+c_{2} w_{2}+c_{3} w_{3} \dots c_{n} w_{n}+b \qquad (2)\)
其中: \(b=b_{1}+b_{2}+b_{3} \ldots b_{n} \qquad (3)\)
因此,每个输入元素有各自的偏置不会对结果造成影响。
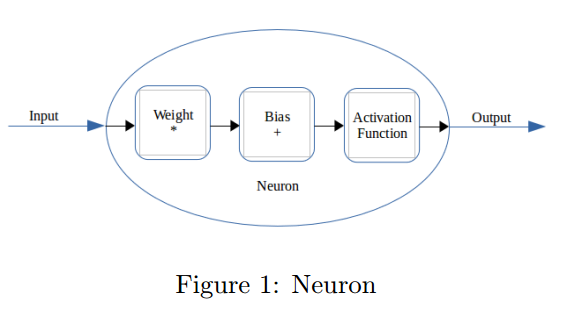
3 The New Backpropagation Algorithm
### 3.1 Calculating new weights and biases for a neuron
我们一次考虑一个神经元,此时有一个输入进入了神经元,即乘以权重加上偏置。这个值通过一个激活函数,激活后的输出就是神经元的输出。
令$C$为输入,原始的权重是$w$,偏置是$b$,$x$为$C$输入后的输出,$x_{n}$是我们要求的输出。基于这个要求,我们需要一个不同的权重和偏置,设为$w_{n}$和$b_{n}$。
原始的输出为: \(C w+b=x \qquad (4)\)
但是我们希望的是: \(C w_{n}+b_{n}=x_{n} \qquad (5)\)
令: \(w_{n}=w-\Delta w \qquad (6)\) \(b_{n}=b-\Delta b \qquad (7)\) 这里$\Delta w$是权重的误差,$\Delta b$是偏置的误差。
\(C w_{n}+b_{n}=x_{n} \qquad (8)\) \(C(w-\Delta w)+(b-\Delta b)=x_{n} \qquad (9)\) \((C w+b)-(C \Delta w+\Delta b)=x_{n} \qquad (11)\) \(x-x_{n}=(C \Delta w+\Delta b) \qquad (12)\)
因此: \(C \Delta w+\Delta b=\left(x-x_{n}\right) \qquad (13)\)
现在: \(\left[\begin{array}{ll}{C} & {1}\end{array}\right] \times\left[\begin{array}{c}{\Delta w} \\ {\Delta b}\end{array}\right]=\left[\begin{array}{l}{\left(x-x_{n}\right)}\end{array}\right] \qquad (14)\) \(\left[\begin{array}{c}{\Delta w} \\ {\Delta b}\end{array}\right]=\left[\begin{array}{ll}{C} & {1}\end{array}\right]^{-1} \times\left[\left(x-x_{n}\right)\right] \qquad (15)\)
但是$\left[\begin{array}{ll}{C} & {1}\end{array}\right]$不是一个方阵。因此我们需要找它的Moore-Penrose伪逆: \(\left[\begin{array}{c}{\Delta w} \\ {\Delta b}\end{array}\right]=\left[\begin{array}{ll}{C} & {1}\end{array}\right]^{+} \times\left[\left(x-x_{n}\right)\right. \qquad (16)\)
在得到$\Delta w$和$\Delta b$后,原始的权重和偏置到新权重和偏置: \(w_{n}=w-(\Delta w * \alpha) \qquad (17)\) \(b_{n}=b-(\Delta b * \alpha) \qquad (18)\) 这里$\alpha$ 是学习率。
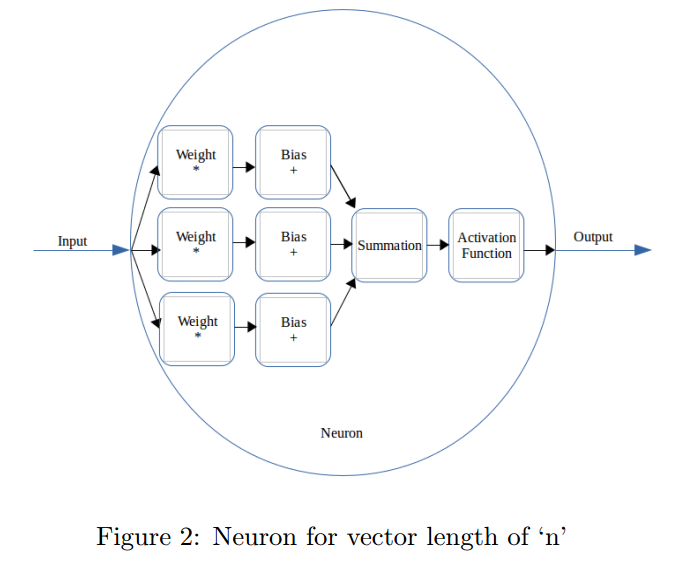
3.2 Tackling multiple inputs
可以令输入$C$为$n^{t h}$维度向量。就可以扩展到多输入情况。此时有n个输入元素,有n个对应的权重和偏置,n个对应的输出。这些输出求和为一个输出,然后输入到激活函数。
在反向传播阶段,期望的输出分发到所有的权重-偏置对上,对于一个权重-偏置块$\left(w_{i}, b_{i}\right)$,期望的输出是总体期望输出的1$/ n$: \(x_{n_{i}}=x_{n} / n \qquad (19)\)
权重和偏置开始时是随机初始化的。每个输入向量中元素对应的权重应该一样。每个权重-偏置块会有相同的输出,这样累积的输出才能给出我们想要的答案。
3.3 Activation Function for non-linearity
通常的方法是用一个非线性函数来做激活函数。在反向传播的时候,我们不能简单的传入希望的输出向量。如果这样做了,权重和偏置的修改会认为好像是没有激活函数一样,这样如果给定相同的输入,那输出也是不对的。因此必须给激活函数的逆函数传入需要的输出向量。我们需要保证选的激活函数让他们的域和范围一样,这样能规避掉数学错误和数据损失。在激活函数逆函数处理后的向量才是我们要传给网络的真实向量。
3.4 Network Architecture
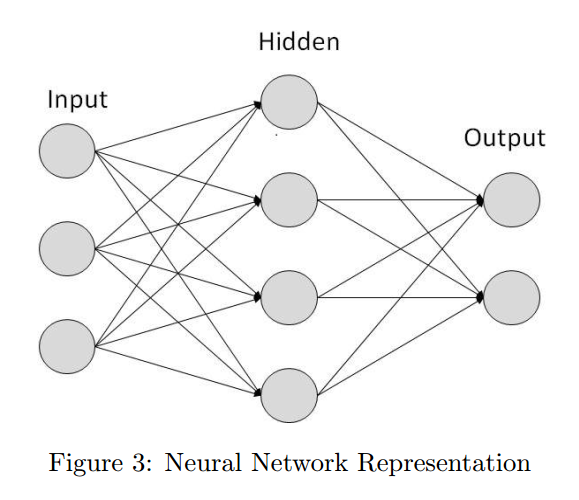
可以转化为下面
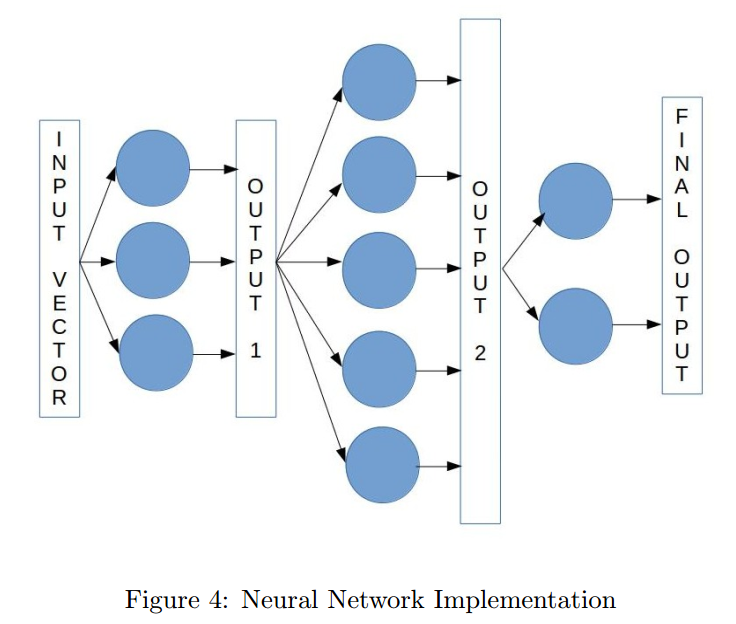
对于最后一层而言,什么样的输入(前一层的输出)可以让这一层的输出是正确的?我们可以得到推导出这个输入向量。
如果: \(C * w+b=x \qquad (20)\) 那么满足$C_{n} * w+b=x$的$C_{n}$为: \(C_{n}=\left(x_{n}-b\right) / w \qquad (21)\) 这些式子可以扩展到前面的层。
另一个问题是,神经元够需要给定自己“要求”的输入向量,这样他们的输出才是正确的。比如多类别分类问题,每个输出向量要求为one-hot编码的向量。因此,我们把所有的向量取平均,这样会给每个神经元相等的权重。再把这些平均的向量传入前面的层作为期望的输出向量。
4 Differences with Extreme Learning Machines
【略】
5 Results
5.1 Telling-Two-Spirals-Apart Problem
Alexis P. Wieland 提出了一个基线任务:区分两个交织在一起的螺旋线。虽然这个任务很直观,但是对于网络来说还是很困难的,因为它极度非线性。
我们使用了包括每类193点的两个螺旋线。我们的网络为16-32-64-32-2,激活为softplus。我们训练了1000个周期,学习率0.0002。
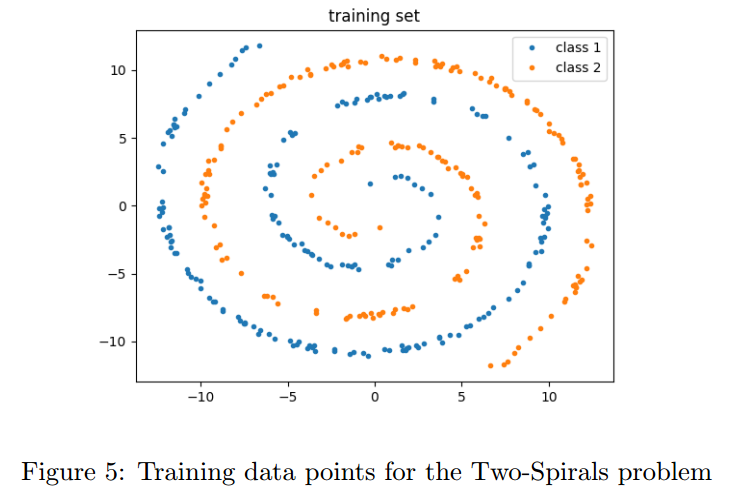
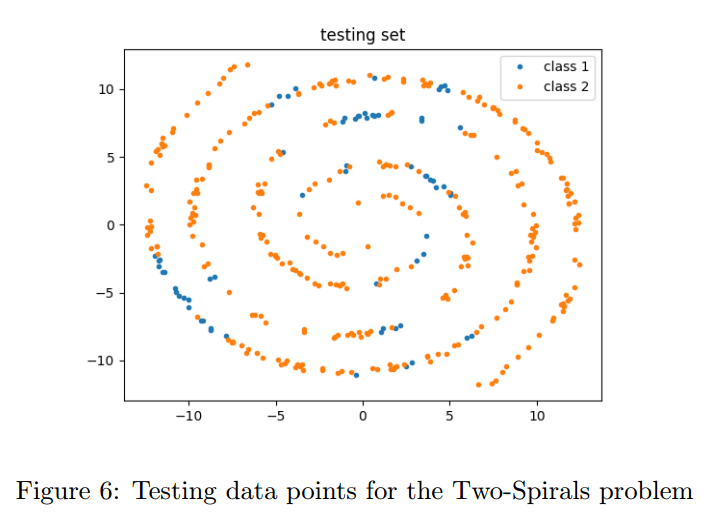
准确率为63%,这是因为softplus的激活函数在这个问题上不好。推荐的激活函数是Tanh,但是由于逆函数的区间在(-1,1),不在$(-\infty,+\infty)$上,在不损失数据的情况下我们的反向传播不能使用。
5.2 Separating-Concentric-Circles Problem
另一个问题是同心环,【略】我们的网络是16-64-32-2,还是使用了softplus。【略】
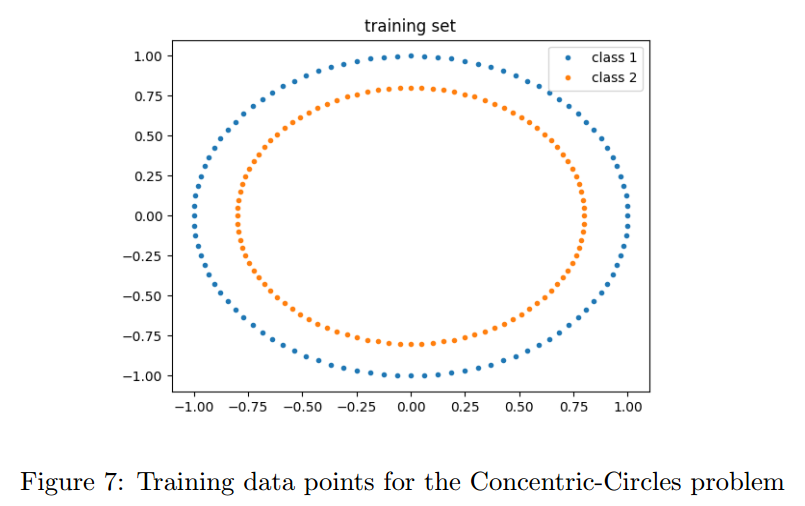
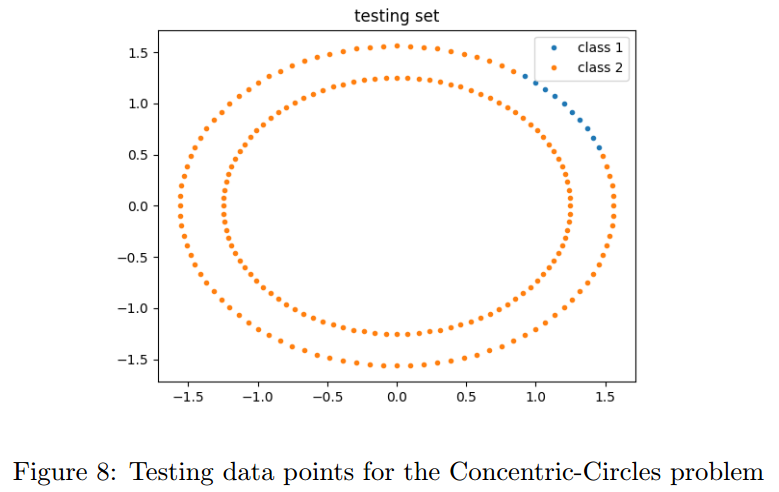
准确率是61%,再一次是softplus的问题。。。
5.3 XOR Problem
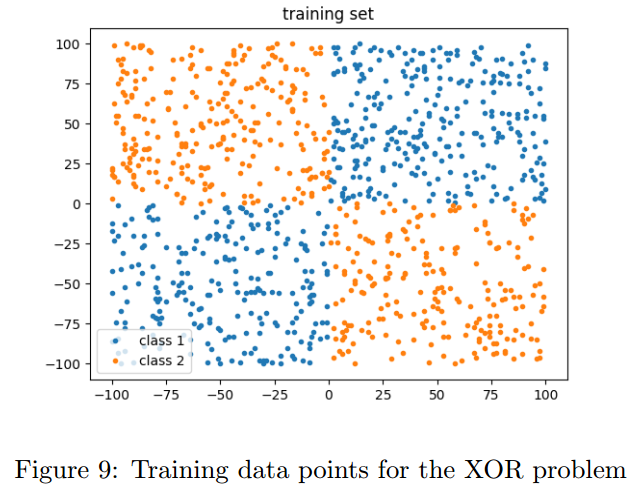
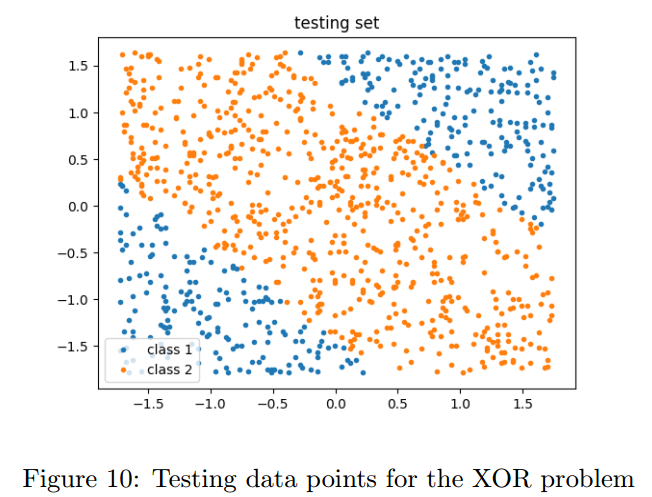
【略】
6 Discussions and Conclusion
【略】没看出来这篇文章的意义