XGBoost: A Scalable Tree Boosting System

Contact me

Blog -> https://cugtyt.github.io/blog/index
Email -> cugtyt@qq.com
GitHub -> Cugtyt@GitHub

本系列博客主页及相关见此处

Abstract

Tree boosting是高效和广泛使用的机器学习算法，本文我们描述了一个可扩展的端到端的Tree boosting系统，叫做XGBoost，可以被广泛用于现在的机器学习算法挑战，达到最好的结果。我们提出了一个新的稀疏感知算法可以用于稀疏数据和稀疏树学习的加权分数位概览。更重要的是我们提供了缓存访问模式、数据压缩和共享的见解，可以构建一个可扩展的Tree boosting系统。把这些见解结合起来，XGBoost可以扩展到亿级别的样本，资源使用比现有的系统更少。

INTRODUCTION

机器学习算法和数据驱动的方法在很多领域变得很重要，有很多应用，这些成功的应用的驱动因素有两点，使用高效的模型捕获复杂的数据依赖，可扩展的模型系统学习大数据集的模型。

在机器学习实践中，梯度tree boosting可以解决很多问题，在很多标准分类基准上达到了最好的结果。

本文我们描述了XGBoost，一个tree boosting的可扩展机器学习系统。它已经在帮助赢得了很多比赛。

这些结果证明了我们的系统在大范围的问题中可以达到最好的效果。虽然领域依赖的数据分析和特征工程非常重要，但是大家对XGBoost的一致选择展示了我们系统和tree boosting的重要性。

XGBoost最重要的因素是所有情境下的可扩展性。系统比很多单机上的解决方案要快10倍以上，可以在分布式或内存受限的情况下扩展到十亿级别的样本。可扩展性是由于几个重要的的系统和算法优化，包括：一种用于解决系数数据的新型学习算法，一个理论上公正加权分位数概览过程可以用树学习解决实例加权。并行和分布式计算可以让学习更快，也可以让模型探索更快。更重要的是，XGBoost探索了核外计算，可以让数据科学家在电脑上处理过亿的样本。最后，把这些技术结合起来做成一个端到端的系统，在最少的资源下扩展到更大的数据，文章主要的贡献是：

我们设计和搭建了一个高度可扩展的端到端tree boosting系统
我们提出了一个理论上公正加权分位数概览用于高效计算
我们引入了一个新的稀疏感知算法用于用于并行树学习
我们提出了一个高效的缓存感知块结构用于核外树学习

TREE BOOSTING IN A NUTSHELL

这个部分我们回顾了tree boosting算法，我们对Friedman的方法做了一点正则目标改进，我们发现实践中是很有帮助的。

Regularized Learning Objective

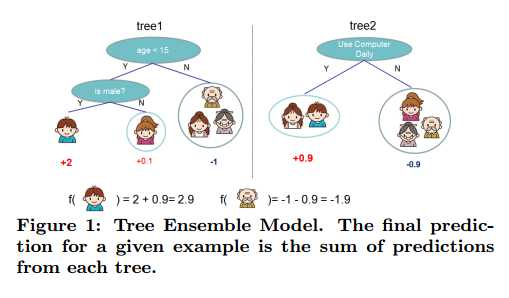
对于一个数据集有n个样本，m个特征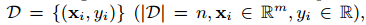， xgboost-eq1 ，一个树的ensemble模型（图1）使用K个额外的函数预测输出：

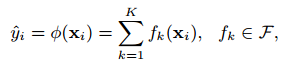
xgboost-eq2

其中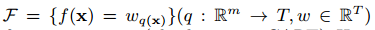 xgboost-eq3 是回归树空间（也叫做CART）。这里q表示每个树的结构，把样本映射到对应的叶子索引，T是叶子数目。每个$f_k$对应于一个独立的树结构q和叶子权重w，不像决策树，每个回归树的叶子包括一个连续分数，我们使用$w_i$表示dii个叶子的分数。对于给定的样本，我们使用树的决策规则来把它分类到叶子上，通过对所有相关叶子分数求和计算最后的预测值。为了学习模型使用的函数集，我们使用了下面的正则化目标：

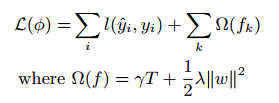
xgboost-eq4

其中l是一个可微的凸损失函数，衡量预测值和真实值之间的差别，第二项$\Omega$是模型复杂度的惩罚。正则化项可以平滑最后的权重以防止过拟合。直觉上，正则化目标倾向于选择一个简单有用的模型。一个相似的正则化方法已经被正则贪心森林(RGF)模型使用。我们的目标和对应的学习算法比RGF更简单，更容易并行。当正则化参数设置为0，目标退化到传统的梯度tree boosting。

xgboost-fig1

Gradient Tree Boosting

树的ensemble模型的公式不能用传统的欧几里得空间的优化方法优化，所以模型用其他的方法训练。严格来讲，令$\hat{y}_i^(t)$为第i次迭代第i个实例预测，我们需要加入$f_t$来最小化目标：

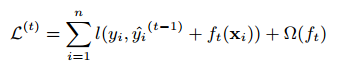
xgboost-eq5

这意味着我们贪心的加入了$f_t$最大的提升了模型。在通常的设定中二阶近似可以快速的优化目标：

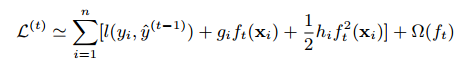
xgboost-eq6

其中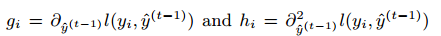 xgboost-eq7 是损失函数的一阶和二阶梯度统计。我们可以移除常数项达到最简化的形式：

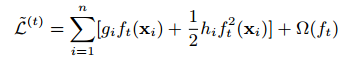
xgboost-eq8

定义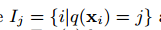 xgboost-eq9 作为叶子j的实例集，我们把$\Omega$展开为：

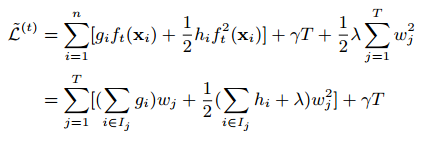
xgboost-eq10

对于一个固定的结构q(x)我们可以计算最优权重为：

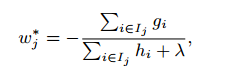
xgboost-eq11

相应的最优值为：

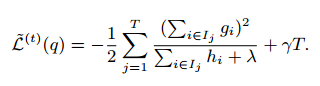
xgboost-eq12

可以用来做分数函数衡量树结构q的质量。这个分数像不纯度，除了它是从更广的目标函数导出的。图2是这个分数是如何计算的。

xgboost-fig2

通常不可能遍历所有可能的树结构q。一个贪心的算法可以从一个简单的叶子开始迭代加入分支。假设$I_L$和$I_R$是划分后的左右叶子的实例集，令$I=I_L \cup I_R$，然后划分后的损失减少为：

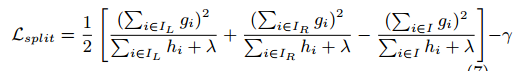
xgboost-eq13

Shrinkage and Column Subsampling

除了正则化目标，两个额外的方法也用于进一步减少过拟合。第一个是收缩，收缩在树boosting后把新加入的权重用一个因子$\eta$来缩放。与随机优化的学习率相似，收缩减少了每个树的影响，把空间留给未来的树以提升模型性能。第二个方法是列下采样，这个方法已经用在随机森林上。根据用户反馈，使用列的下采样比传统的行采样更能防止下采样，这个方法也加速了并行计算。

SPLIT FINDING ALGORITHMS

Basic Exact Greedy Algorithm

树学习一个关键的问题是找到最好的划分。一个划分寻找算法是穷举所有可能的划分。我们把它叫做精确贪心算法，大部分现有的单机树boosting实现，例如sklearn,R的gbm和单机版本的XGBoost支持精确贪心算法。精确贪心算法见算法1。为了更高效，算法先把数据根据特征值排序，然后计算结构分数的梯度统计。

xgboost-algo-1-2

Approximate Algorithm

精准贪心算法是很厉害的，因为它穷举了所有的可能划分。但是如果数据无法全部读入内存，他就无法高效实现，在分布式中也一样。为了在这两种情况下高效支持梯度树boosting，我们需要一个近似0的算法。

我们汇总了一个近似的框架，可以把以前的点子集成在一起，算法2。为了汇总，算法先根据特征分布百分数处理分割候选点。然后算法把连续特征映射到候选点分割的存储中，对统计聚合，找到最好的解法。

有两个算法的变种，取决于什么时候提议给定。全局变种在构建树的初始阶段提出所有的候选分割，在所有的分割搜索上使用相同的提议。局部变种在分割后重新提议。全局的方法需要更少的提议步骤。但是使用更多的候选点，因为候选在每次分割后没有微调。局部提议每次分割后微调了候选，对于更深的树可以潜在的更加精确。图3是在不同算法的比较。我们发现局部提议的确需要更少的候选。全局提议在足够多的候选下准确率可以和局部提议接近。

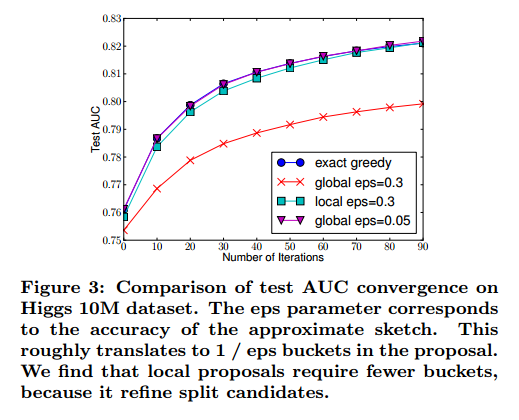
xgboost-fig3

大部分现有的分布式树学习近似算法服从这个框架。值得注意的是，直接构建梯度统计近似直方图是可能的。除了分位数其他binning策略的变种也是可行的。从图3我们也发现分位数策略可以达到相同的准确率，条件是精确贪心给定合理的近似层次。

我们的系统高效的支持单机设置的精确贪心，和所有设定的局部和全局提议方法的近似算法。

Weighted Quantile Sketch

近似算法中一个重要的步骤是提议候选分割点。通常一个特征的分位数是用来让候选分布均匀。严格的，令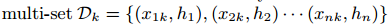 xgboost-eq14 表示第k个特征值和每个训练实例的二阶梯度统计，我们可以定义一个秩函数

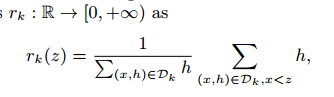
xgboost-eq15

表示特征值k小于z的实例比例。目标是找一个候选分割点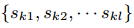 xgboost-eq16 ，使得

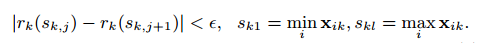
xgboost-eq17

这里$\epsilon$是一个近似因子。直觉上，这意味着大约$1/\epsilon$的候选点。每个数据点权重为$h_i$，为了说明为什么表示权重，我们可以写作：

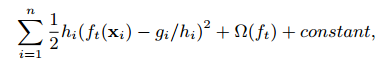
xgboost-eq18

这完全是加权平方损失，对于大的数据集，找到一个满足要求的候选分割不简单。当每个实例有一样的权重时，一个现有的算法时分位点草图解决这个问题。但是没有分位草图用于加权数据集。因此，一些现有的近似算法或对一个数据的随机子集排序，但是有可能失败，或者启发式的方法但是缺乏理论保证。

为了解决这个问题，我们引入了一个新的分布式加权分位数草图算法可以解决加权数据，而且有理论保证。通常的主意是提出一个数据结构可以支持合并和修建操作，每个操作保持一个确定的准确度。

Sparsity-aware Split Finding

在很多真实世界问题中，输入X是稀疏的是很常见的。有很多可能的原因：1）数据中的缺失值，2）统计中频繁的0值，3）人工特征提取，例如one-hot。算法的稀疏感知是很重要的。为了做到这点，我们提出对每个树节点加入一个默认的方向，见图4。当输入矩阵X的值是缺失的，实例分类到默认的方向。最优的方向是从数据中学到的。算法见算法3。关键的改进是只访问非缺失的实体。展示的算法对待没出现的值为缺失值，学习处理缺失值最好的方法。相同的算法可以用于用户指定的值不出现，限制穷举到一致的解法。

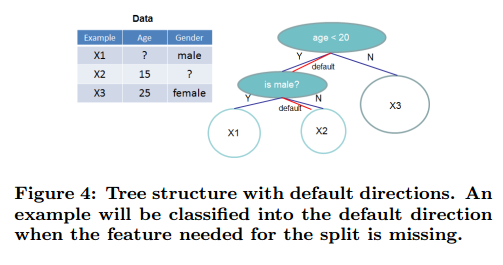
xgboost-fig4 xgboost-algo3

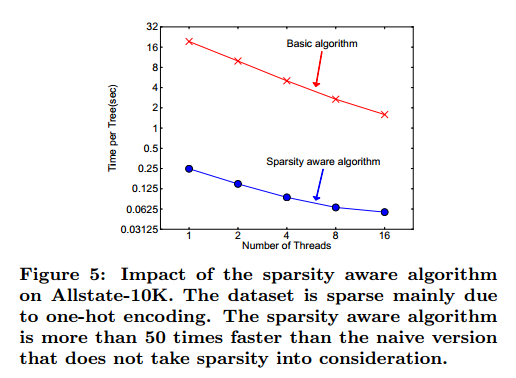
就我们所知，大部分现有的树学习算法或只对密集数据优化，或需要特殊的步骤来处理受限的情况，例如类别编码。XGBoost用同一的方法来处理稀疏的情况。更重要的是我们的方法对稀疏情况的探索可以让计算复杂度和非丢失值线性相关。图5是稀疏感知和普通实现的比较。我们发现稀疏感知算法比普通版本快50倍。

xgboost-fig5

SYSTEM DESIGN

Column Block for Parallel Learning

树学习最大的消耗是将数据排序。为了减少排序的消耗，我们提出把数据存入内存单元，我们称作块。块中的数据使用压缩列（compressed column，CSC）格式存储，每列把对应的特征值排序。这个输入数据只需要在训练前计算一次，在后面的迭代中重复利用。

在精确贪心算法中，我们把整个数据集存到一个块中，对已经排好序的实体通过线性扫描运行分割搜索算法。我们对所有的叶子共同做分割查找，所以一次查找可以收集所有叶子分支的分割候选的统计。图6显示了我们如何把数据转为对应的格式，和使用块结构找到最优划分。

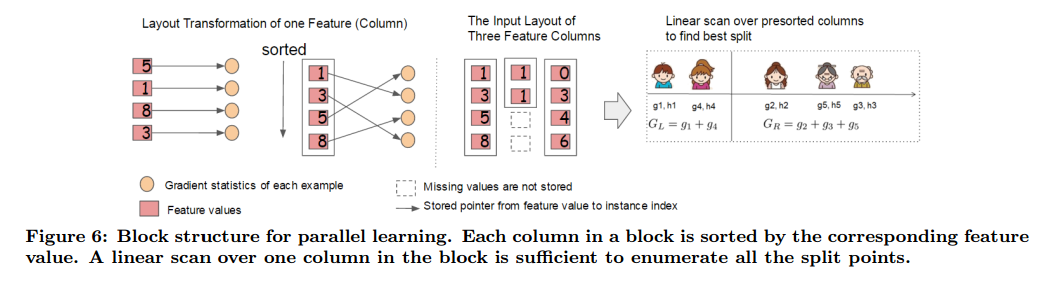
xgboost-fig6

在使用近似算法时，块结构也有帮助。这种情况下可以使用多个块，每个快对应于数据集中的行子集。不同的块可以在多机上分布，或者使用核外设置存储到硬盘中。使用排好序的结构，分位数查找步骤可以变成线性扫描。这对于局部提议算法来说更有价值，候选在每个分支频繁的生成。二分搜索直方图聚合也可以变成线性合并算法。

收集每列的统计可以是并行的，这让我们可以用并行算法来做分割查找。重要的是，列块结构也支持列下采样，很容易在块中选择一个列的子集。

Time Complexity Analysis令d为数的最大深度，K为树的个数。对于精确贪心算法，原始稀疏感知算法的时间复杂度是$O(Kd \lVert x \rVert_0 \log n)$,这里我们使用$\lVert x \rVert_0$来表示无缺失实体的数量，另外，块结构中树boosting只需要$O(Kd \lVert x \rVert_0 + \lVert x \rVert_0\log n)$，这里$\lVert x \rVert_0 \log n$是一次的处理损耗，可以被分摊。这个分析说明块结构帮助节约了logb的部分，n很大是尤其明显。对于近似算法，使用二分查找的原始算法时间复杂度是$O(Kd \lVert x \rVert_0 + \lVert x \rVert_0\log q)$。q是数据集的提议候选数。q通常在32到100之间。使用块结构，我们可以减少时间到$O(Kd \lVert x \rVert_0 + \lVert x \rVert_0\log B)$，这里B是每个块的最大行数。再一次我们可以额外的log q。

Cache-aware Access

虽然块结构帮助优化了分割搜索的计算复杂度，新的算法需要通过行索引间接获取梯度统计，因为这些值是按照特性来访问的。这是非连续的内存访问。一个分割穷举的简单实现引入了积累和非连续内存获取操作之间的及时读写依赖（见图8），这降低了梯度统计不能放入CPU缓存或缓存丢失情况下分割查找的速度。

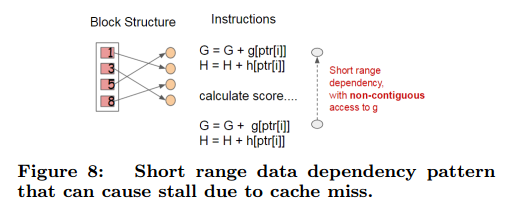
xgboost-fig8

对于精确贪心算法，我们可以通过缓存感知获取算法来减缓这个问题。特别的，我们在每个线程分配一个内部缓存，在其中获取梯度统计值，然后在一个小批量上执行累积操作。预读取操作转变直接读写依赖为更长的依赖，在行数很大时帮助减少了运行开支。图7是缓存感知和非缓存感知在Higgs和Allstate数据集的比较。我们发现精确贪心算法的缓存感知实现比普通方法快2倍。

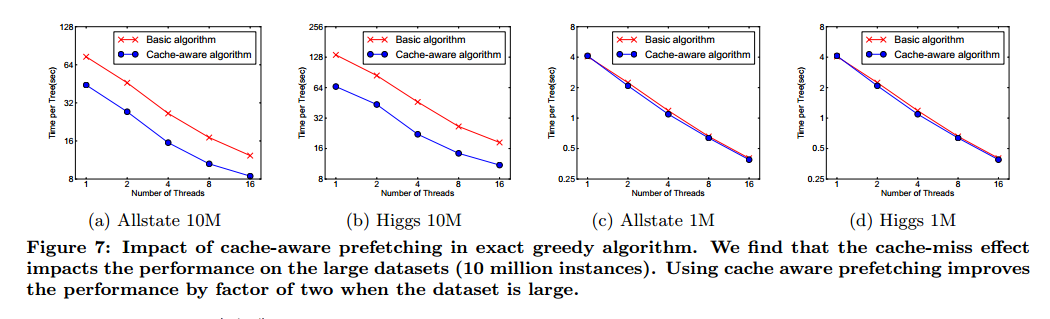
xgboost-fig7

对于近似算法，我们通过选择合适的块大小来解决这个问题，我们反映出块大小为块最大容纳的样本数量，这反映了梯度统计值的缓存损失。选择一个很小的块导致每个线程很小的负荷，并行效率不高。另一方面，大的块在梯度统计无法放入CPU导致缓存丢失。好的选择需要平衡这两个因素，我们比较了块大小的选择，结果在图9中，结果验证了我们的想法，选择2^16是合适的。

Blocks for Out-of-core Computation

我们目标是系统可以完全利用机器资源来达到可扩展的学习。除了处理器和内存，使用硬盘空间来处理无法放入内存的问题也是很重要的。为了能够做核外计算，我们把数据分成多个块，每个块存入硬盘中。在计算的时候，使用独立线程预读取到主内存缓存是很重要的，这样计算可以并发。但是这个没有完全解决问题，因为硬盘读取占用了大量的计算时间。为了减少消耗增加IO的通量，我们主要使用两个方法来提升核外计算。

Block Compression第一个方法是块压缩，通过列来压缩，通多独立的线程解压。我们使用了通用的压缩算法来压缩特征值，对于行索引，我们以行索引取子集。

Block Sharding第二个方法是在多个硬盘之间以轮换的方式共享内存。

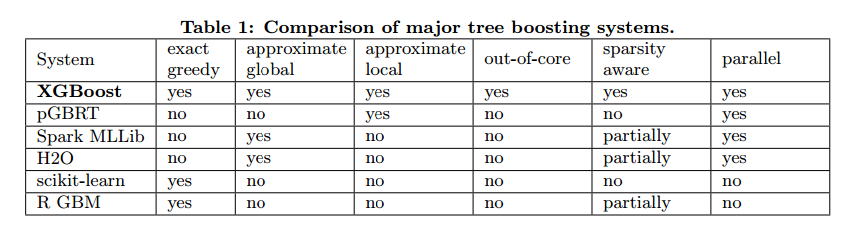
xgboost-tab1

END TO END EVALUATIONS

System Implementation

【略】

Dataset and Setup

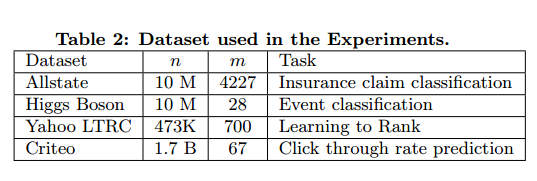
xgboost-tab2

Classification

我们实验了单机上使用精确贪心算法在Higgs-1M数据的XGBoost性能，和其他两个精确树boosting实现做了比较。结果在表3中。

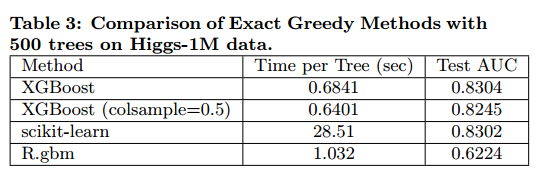
xgboost-tab3

Learning to Rank

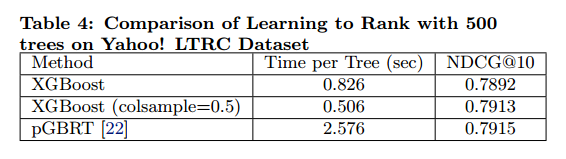
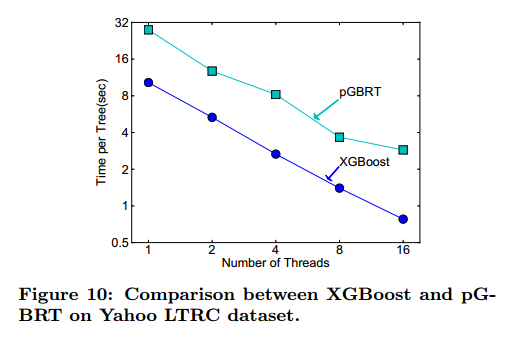
我们实验了学习排列问题中XGBoost的性能，结果见表4和图10。

xgboost-tab4 xgboost-fig10

Out-of-core Experiment

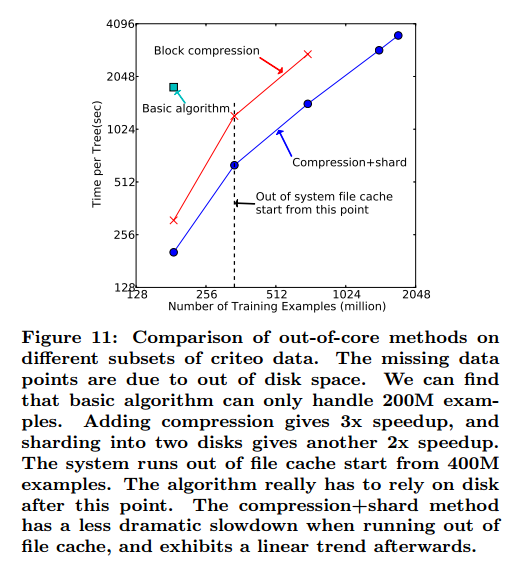
我们比较了在核外设置下criteo数据的结果。结果见图11。

xgboost-fig11

Distributed Experiment

结果见图12。我们发现XGBoost运行更快。

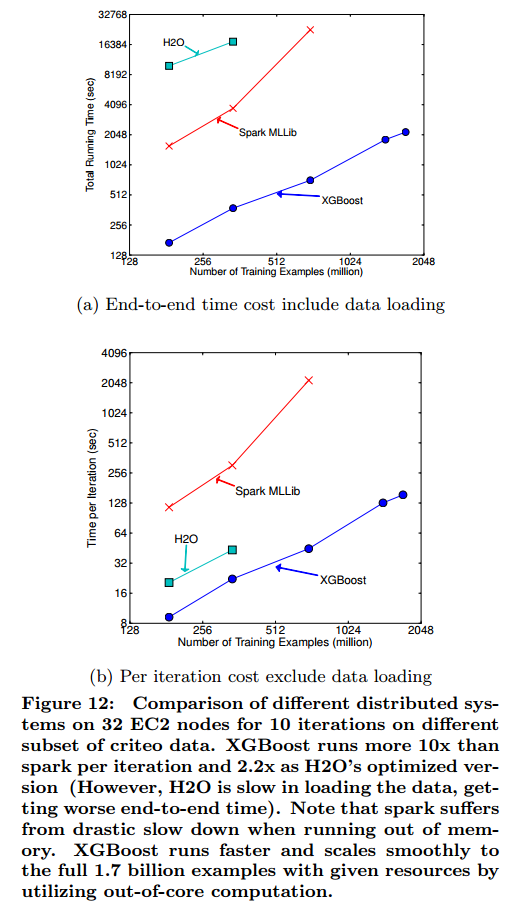
xgboost-fig12

我们也实验了不同机器数量下系统的可扩展性，见图13。

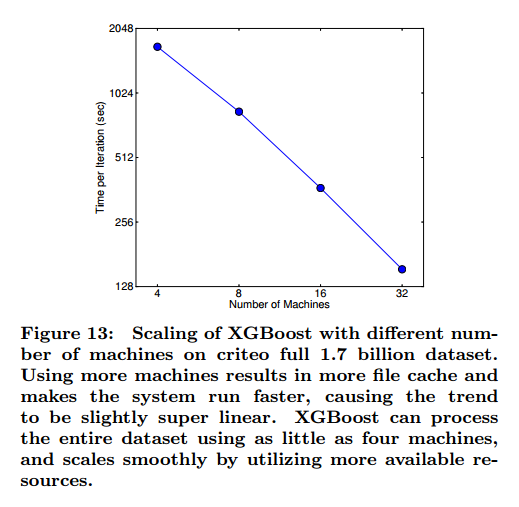
xgboost-fig13

CONCLUSION

我们描述了在构建XGBoost中的一些经验，我们提出了一个新的稀疏感知算法用于处理稀疏数据，和一个理论上公平加权的用于近似学习的分位数概览。我们的实验证明了缓存访问模式，数据压缩，和共享是构建一个可扩展的端到端树boosting系统的关键因素。