leetcode [802] 找到最终的安全状态

---

Contact me:

Blog -> https://cugtyt.github.io/blog/index
Email -> cugtyt@qq.com
GitHub -> Cugtyt@GitHub

---

在有向图中, 我们从某个节点和每个转向处开始, 沿着图的有向边走。 如果我们到达的节点是终点 (即它没有连出的有向边), 我们停止。

现在, 如果我们最后能走到终点，那么我们的起始节点是最终安全的。 更具体地说, 存在一个自然数 K, 无论选择从哪里开始行走, 我们走了不到 K 步后必能停止在一个终点。

哪些节点最终是安全的？ 结果返回一个有序的数组。

该有向图有 N 个节点，标签为 0, 1, …, N-1, 其中 N 是 graph 的节点数. 图以以下的形式给出: graph[i] 是节点 j 的一个列表，满足 (i, j) 是图的一条有向边。

示例：

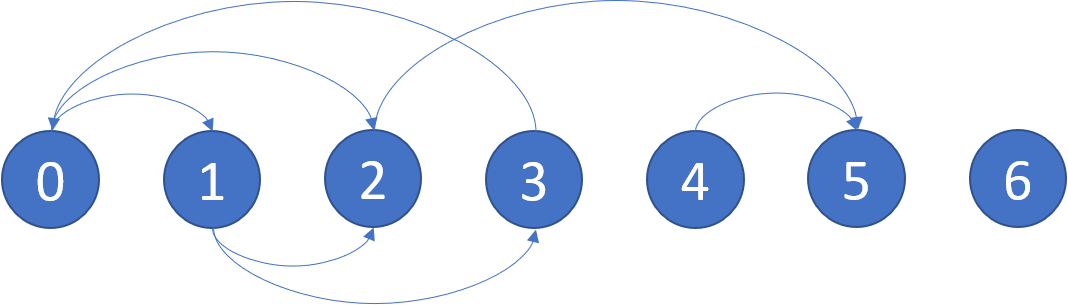
输入：graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出：[2,4,5,6]

这里是上图的示意图。

提示：

graph 节点数不超过 10000.
图的边数不会超过 32000.
每个 graph[i] 被排序为不同的整数列表， 在区间 [0, graph.length - 1] 中选取。

思路：

找到出度为0的节点，记录，删除，重复以上，记录的节点排序即可得到。

class Solution:
    def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float:
        edges = [sorted(edge) for edge in edges]
        edges.sort()
        index = -1
        edges.insert(0, [0, 1])
        for i in range(len(edges)):
            if edges[i][1] == target:
                index = i
                break
        if index == -1:
            return 0
        
        parent = edges[index][0]
        index_, parent_ = index, parent
        prob = 1
        while parent != 0:
            t -= 1
            left, right = index, index
            while left >= 0 and edges[left][0] == parent:
                left -= 1
            while right < len(edges) and edges[right][0] == parent:
                right += 1
            left = left + 1
            prob *= 1 / (right - left)
            for i in range(left - 1, -1, -1):
                if edges[i][1] == parent:
                    index = i
                    parent = edges[i][0]
                    break

        if t < 0: return 0
        if t == 0: return prob
        if t > 0:
            for i in range(index_, len(edges)):
                if edges[i][0] == target:
                    return 0
            return prob