leetcode [31] 下一个排列

---

Contact me:

Blog -> https://cugtyt.github.io/blog/index
Email -> cugtyt@qq.com
GitHub -> Cugtyt@GitHub

---

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。

1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

思路来自题解

首先，我们观察到对于任何给定序列的降序，没有可能的下一个更大的排列。

例如，以下数组不可能有下一个排列：

[9, 5, 4, 3, 1]

我们需要从右边找到第一对两个连续的数字 a[i]a[i]a[i] 和 a[i−1]a[i-1]a[i−1]，它们满足 a[i]>a[i−1]a[i]>a[i-1]a[i]>a[i−1]。现在，没有对 a[i−1]a[i-1]a[i−1] 右侧的重新排列可以创建更大的排列，因为该子数组由数字按降序组成。因此，我们需要重新排列 a[i−1]a[i-1]a[i−1] 右边的数字，包括它自己。

现在，什么样子的重新排列将产生下一个更大的数字呢？我们想要创建比当前更大的排列。因此，我们需要将数字 a[i−1]a[i-1]a[i−1] 替换为位于其右侧区域的数字中比它更大的数字，例如 a[j]a[j]a[j]。

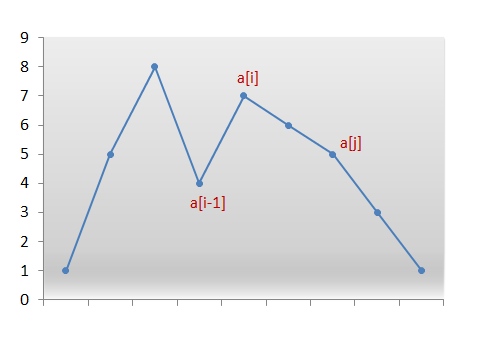
我们交换数字 a[i−1]a[i-1]a[i−1] 和 a[j]a[j]a[j]。我们现在在索引 i−1i-1i−1 处有正确的数字。 但目前的排列仍然不是我们正在寻找的排列。我们需要通过仅使用 a[i−1]a[i-1]a[i−1]右边的数字来形成最小的排列。 因此，我们需要放置那些按升序排列的数字，以获得最小的排列。

但是，请记住，在从右侧扫描数字时，我们只是继续递减索引直到我们找到 a[i]a[i]a[i] 和 a[i−1]a[i-1]a[i−1] 这对数。其中，a[i]>a[i−1]a[i] > a[i-1]a[i]>a[i−1]。因此，a[i−1]a[i-1]a[i−1] 右边的所有数字都已按降序排序。此外，交换 a[i−1]a[i-1]a[i−1] 和 a[j]a[j]a[j] 并未改变该顺序。因此，我们只需要反转 a[i−1]a[i-1]a[i−1] 之后的数字，以获得下一个最小的字典排列。

下面的动画将有助于你理解：

class Solution:
    def nextPermutation(self, nums: List[int]) -> None:
        i = len(nums) - 2
        while i >= 0 and nums[i + 1] <= nums[i]:
            i -= 1
        if i >= 0:
            j = len(nums) - 1
            while j >= 0 and nums[j] <= nums[i]:
                j -= 1

            nums[i], nums[j] = nums[j], nums[i]
        
        nums[i + 1:] = nums[i + 1:][::-1]