图的最长路径 –BFS,树,图
Contact me:
Blog -> https://cugtyt.github.io/blog/index
Email -> cugtyt@qq.com
GitHub -> Cugtyt@GitHub
给定一个图,求图中的最长路径(或称直径),例如
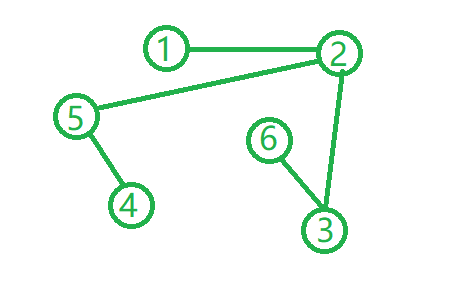
其中节点之间最长的路径是:6-3-2-5-4,路径长4,最简单粗暴的方法是,遍历所有的节点与节点之间的距离,看最后最长的路径是多少:
constexpr size_t len = 6;
vector<vector<int>> map = {
// 1 2 3 4 5 6
{999, 1, 999, 999, 999, 999}, // 1
{1, 999, 1, 999, 1, 999}, // 2
{999, 1, 999, 999, 999, 1}, // 3
{999, 999, 999, 999, 1, 999}, // 4
{999, 1, 999, 1, 999, 999}, // 5
{999, 999, 1, 999, 999, 999}, // 6
};
// 三重遍历,计算所有点之间的距离
for (auto i = 0; i < len; ++i) {
for (auto j = 0; j < len; ++j) {
for (auto k = 0; k < len; ++k) {
map[j][k] = min(map[j][k], map[j][i] + map[i][k]);
}
}
}
int maxlen = 0;
for (auto i = 0; i < len; ++i) {
for (auto j = 0; j < len; ++j) {
maxlen = max(maxlen, map[i][j]);
}
}
cout << "max length = " << maxlen << "\n";
三重遍历,主要就是计算所有点之间的距离,i到j的距离是map[j][k]和map[j][i]+map[i][k]中的最小值。通过三重遍历,可以得到一个新的距离矩阵:
#1 #2 #3 #4 #5 #6
2 1 2 3 2 3 #1
1 2 1 2 1 2 #2
2 1 2 3 2 1 #3
3 2 3 2 1 4 #4
2 1 2 1 2 3 #5
3 2 1 4 3 2 #6
其中的最大值就是图的直径。
上面方法的复杂度是O(n^3),为了减少时间复杂度,我们这样考虑,先把图的遍历过程看作是一个遍历树,起点随机:
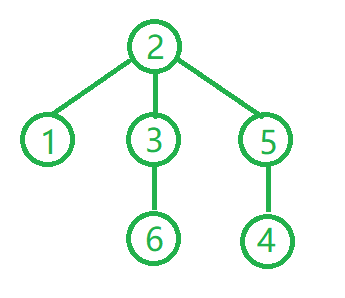
但是最长直径的遍历树(记作最高遍历树)是这样,4和6都可以作为根节点:
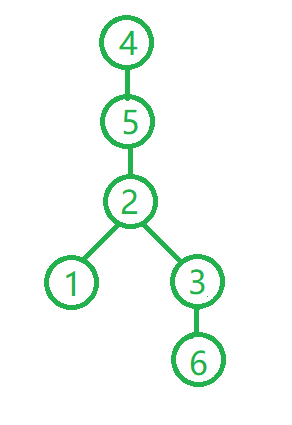
这里强调:遍历树的根节点肯定在最高遍历树上(废话),而且该节点遍历的最深的叶子节点肯定是最高遍历树的根节点(可能有多个) 可以看成,随机选取的节点就是从最高遍历树中的某个节点开始进行搜索的,就像图中的节点2。基于这个结论,我们可以这样做:随机选取一个节点,广度优先遍历(这样可以知道哪些节点层数最深),找到深度最深(最后遍历)的节点,多个的话可以随机选一个,然后基于这个最后的节点为起始节点,重新进行遍历,记录层数,就是图的直径了。
#include <queue>
#include <vector>
using namespace std;
// 记录访问与否
vector<bool> visited;
// 存图
vector<vector<int>> map;
// 广度优先使用的队列,每个元素包括节点和层数
queue<pair<int, int>> q;
// 记录第一次遍历最后的节点
int last;
// current 就是当前遍历的节点, maxlen 是当前遍历节点的层数
int BFS(int current, int maxlen) {
// 记录访问过
if (!visited[current]) {
visited[current] = true;
}
// 对于每个邻居,压入队列
for (auto i = 0; i < map[current].size(); ++i)
{
if (!visited[i] && map[current][i])
{
q.push(make_pair(i, maxlen));
}
}
// 不为空,表示还在继续处理,对队列中的头一个进行BFS
if (!q.empty())
{
auto [top, len] = q.front();
q.pop();
return BFS(top, len + 1);
}
// 为空表示搜索结束,记录最后的节点,返回当前层数
else
{
last = current;
return maxlen;
}
}
int main() {
// init states
constexpr size_t len = 6;
visited = vector<bool>(len, false);
map = {
// 1 2 3 4 5 6
{0, 1, 0, 0, 0, 0}, // 1
{1, 0, 1, 0, 1, 0}, // 2
{0, 1, 0, 0, 0, 1}, // 3
{0, 0, 0, 0, 1, 0}, // 4
{0, 1, 0, 1, 0, 0}, // 5
{0, 0, 1, 0, 0, 0}, // 6
};
// 随机选一个起始点访问
BFS(2, 0);
// 清空访问,再次遍历得到返回的最大层数
visited = vector<bool>(len, false);
auto maxlen = BFS(last, 0);
cout << "max length = " << maxlen << "\n";
}
max length = 4
随便加一条边:
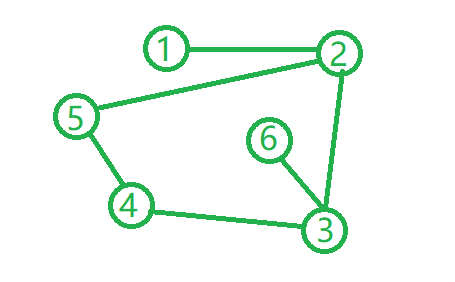
max length = 3