找到出现多次的数

Contact me:

Blog -> https://cugtyt.github.io/blog/index
Email -> cugtyt@qq.com
GitHub -> Cugtyt@GitHub

Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.

Note:

You must not modify the array (assume the array is read only).

You must use only constant, O(1) extra space.

Your runtime complexity should be less than O(n2).

There is only one duplicate number in the array, but it could be repeated more than once.

第一条限制，不能修改数组。这导致我们不能借用排序等手法将复杂度限制在nlogn情况下。否则我们只要排序一遍，然后遍历一遍即可解出答案。

第二条限制，只能使用O(1)的空间。这导致我们不同借用任何存储的方法，也就是不能使用计数、有记忆的方法。否则我们可以使用计数器，找到出现多于一次的数字，为了节省空间，考虑到只是多于1次，那么可以用位存储。

第三条限制，时间复杂度低于O(n^2)。这导致我们不同使用两层循环求解。否则我们只需要两个循环，进行n^2遍历，即可找到答案。

第四条限制，只有一个重复数，但是可能出现多次。看似不是限制，但是这导致我们不能用数字规律简答求解，如果只出现2次，那么可以用等差数列和与实际求和结果求差即可解答。

因此，问题不能直接从数字规律本身，和记录统计等方法，这里会用到一个特殊的方法，求序列中的环的思想，详细解释看找到链表中的环，下面是简单解释。

先来看下这个思想是什么意思，考虑一个链表，但是可能出现环，最简单就是循环链表，首尾相接，但也可能是中间一部分出现环：

寻找的方法这里给出，就是两个指针，一快一慢，都从链表第一个和第二个开始，慢的指针一次向后走一步，快的一次向后走两步。那么可以证明的是如果有环，那么这两个指针会在某一时刻到达同样的位置。这里不详细说明。

那么这个问题和题目有什么关系？考虑给定数组中数的特殊性，n+1个范围在1-n的数字，那么每个数字作为索引的话可以到达任意位置并且不会越界。我们把它想象为链表中的地址，这里需要指针和地址概念清楚，那么可想而知，如果出现了重复数字，就相当于出现了环。

例如数组：

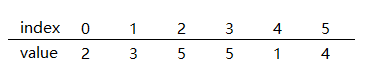
5出现了两次，我们把index当作链表单元自己的地址，value当作下一个单元的地址，从0单元开始，这样就如下图所示：

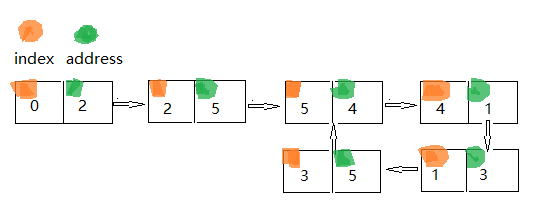
可以看到当多个数字出现时，肯定出现了环，那么就可以用上面我们所介绍的思想去解决。

具体程序（来自网络解答）：

int findDuplicate3(vector<int>& nums) {
    if (nums.size() > 1) {
        int slow = nums[0];
        int fast = nums[nums[0]];
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[nums[fast]];
        }
        fast = 0;
        while (fast != slow) {
            fast = nums[fast];
            slow = nums[slow];
        }
        return slow;
    }
    return -1;
}

程序和找到链表中的环基本一样，可以看链接详细理解。