Michael Nielsen对梯度消失的解释（二）

Contact me:

Email -> cugtyt@qq.com
GitHub -> Cugtyt@GitHub

为了理解为什么梯度消失问题会出现，我们先考虑最简单的深度神经网络：每层只有一个神经元。这是一个三隐层网络：

$w_1, w_2, \ldots$ 表示weights， $b_1, b_2, \ldots$ 表示biases，C是损失函数。第j个神经元的输出 $a_j$ 是 $\sigma(z_j)$ , $z_j = w_{j} a_{j-1}+b_j$ 是加权输入。损失函数C是网络的输出 $a_4$ 的函数：如果实际输出接近期望输出，损失函数很小，如果相差很远，损失函数很大。

继续说第一隐层的梯度 $\partial C / \partial b_1$ ，通过这个表达式我们会理解为什么梯度消失的问题会出现。

先看 $\partial C / \partial b_1$ 的表达式，看起来有点可怕，但这的确是个简单的结构：

想象我们在 $b_1$ 上一个小的变化 $\Delta b_1$ ，这回导致一系列的变化。首先第一隐层神经元的输出变化 $\Delta a_1$ ，然后第二隐层的加权输入变化 $\Delta z_2$ ，第二隐层的输出变化 $\Delta z_2$ ，一直到损失函数变化 $\Delta C$ ，我们有：

$\frac{\partial C}{\partial b_1} \approx \frac{\Delta C}{\Delta b_1}$

因此我们可以小心的跟踪每一步观察 $\partial C / \partial b_1$ 的变化。

首先思考 $\Delta b_1$ 是如何导致第一隐层输出 $a_1$ 变化的，我们有 $a_1 = \sigma(z_1) = \sigma(w_1 a_0 + b_1)$ ，因此：

$\Delta a_1 \approx \frac{\partial \sigma(w_1 a_0+b_1)}{\partial b_1} \Delta b_1 \ = \sigma'(z_1) \Delta b_1$

$\sigma'(z_1)$ 这一项和 $\Delta b_1$ 产生了激活输出变化 $\Delta a_1$ ，这个变化反过来导致第二隐层的加权输入 $z_2 = w_2 a_1 + b_2$ 变化：

$\Delta z_2 \approx \frac{\partial z_2}{\partial a_1} \Delta a_1 = w_2 \Delta a_1$

结合 $\Delta z_2$ 和 $\Delta a_1$ ，我们看 $b_1$ 的变化影响到 $z_2$ ：

$\Delta z_2 & \approx & \sigma'(z_1) w_2 \Delta b_1$

我们可以继续做下去，跟踪剩下的改变。最后的表达式是：

$\Delta C \approx \sigma'(z_1) w_2 \sigma'(z_2) \ldots \sigma'(z_4) \frac{\partial C}{\partial a_4} \Delta b_1$

除以 $\Delta b_1$ 得到：

$\frac{\partial C}{\partial b_1} = \sigma'(z_1) w_2 \sigma'(z_2) \ldots \sigma'(z_4) \frac{\partial C}{\partial a_4}$

为什么梯度消失问题出现？让我们写出完整的表达式：

$\frac{\partial C}{\partial b_1} = \sigma'(z_1) \, w_2 \sigma'(z_2) \, w_3 \sigma'(z_3) \, w_4 \sigma'(z_4) \, \frac{\partial C}{\partial a_4}$

除了最后一项，表达式是多个形如 $w_j \sigma'(z_j)$ 的积，我们看下 $\sigma'$ 的图像：

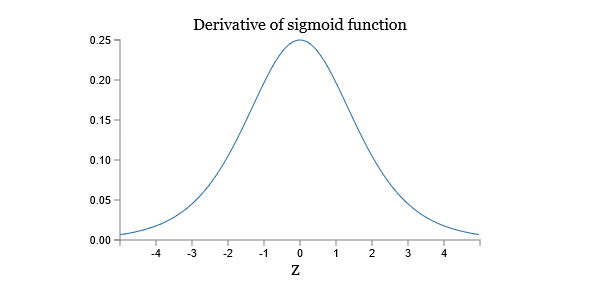
导数最大值为 $\sigma'(0) = 1/4$ 。现在如果我们使用均值为0，方差为1的高斯分布初始化weights，weights通常满足 $|w_j| < 1$ ，放在一起， $w_j \sigma'(z_j)$ 项通常满足 $|w_j \sigma'(z_j)| < 1/4$ ，把这些项乘起来，结果就会指数级的减小：项越多，积越小。这就是梯度消失的一个可能解释了。

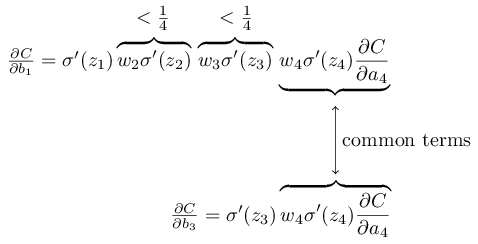
为了更明显些，让我们比较 $\partial C / \partial b_1$ 和 $\partial C / \partial b_3$ ：

这两个表达式有很多共同的部分，但是上面的表达式多两个 $w_j \sigma'(z_j)$ 项，因此 $\partial C / \partial b_1$ 通常是 $\partial C / \partial b_3$ 的1/16，也就是梯度消失的源头。

当然这是一个非正式的论点，并非严格证明梯度消失问题将会发生。有几个可能的例外，我们可能会怀疑weights可以在训练期间增长。发生时 $w_j \sigma'(z_j)$ 不再满足 $|w_j \sigma'(z_j)| < 1/4$ ，如果这些项足够大（大于1）那么就会出现梯度爆炸的问题。

梯度爆炸问题：让我们看一个梯度爆炸出现的例子，这个例子是人为的：我将会调整参数让梯度爆炸出现。即便是人为的，它也可以说明梯度爆炸的确会出现，而不是只有理论可能。

两步出现梯度爆炸，第一，选择很大的weights，比如 $w_1 = w_2 = w_3 = w_4 = 100$ ，第二选择biases让 $\sigma'(z_j)$ 项不要太小。很简单就做到了：我们只需要选择biases保证加权输入 $z_j = 0$ （因此 $\sigma'(z_j) = 1/4$ ），比如我们希望 $z_1 = w_1 a_0 + b_1 = 0$ ，可以设置 $b_1 = -100 * a_0$ ，同样设定其他的biases，做完后，可以看到 $w_j \sigma'(z_j)$ 等于 $100 * \frac{1}{4} = 25$ ，我们这样就得到了梯度爆炸。

梯度不稳定问题：这里的根本问题不是梯度消失和梯度爆炸。因为前面层是后面层各项的乘积，当层数很多时，就会有内在的不稳定情况。所有层次都能以接近相同的速度学习的唯一方法是乘积项接近平衡。因为没有这种平衡发生的机制或内在原因，发生这种情况的可能性就是随机的。简而言之，这里真正的问题是神经网络存在一个不稳定的梯度问题。如果我们使用标准的基于梯度的学习方法，网络中的不同层次将倾向于以非常不同的速度学习。

梯度消失的普遍性：我们已经接触了梯度消失和梯度爆炸，事实上，使用sigmoid通常是梯度消失。考虑表达式 $|w \sigma'(z)|$ ，为了避免梯度消失，我们需要 $|w \sigma'(z)| \geq 1$ 。你也许会认为当w很大时很容易发生，但是要困难得多。原因是 $\sigma'(z)$ 依赖于w： $\sigma'(z) = \sigma'(wa +b)$ 。所以当我们让w很大，我们需要很小心的注意没有同时让 $\sigma'(wa+b)$ 变小。限制很多，因为w很大很容易wa+b很大， $\sigma'$ 就会很小。避免的唯一方法是激活输入落入非常小的范围内，有时候会发生，但是通常不会，因此通常我们遇到的是梯度消失。

我们已经看到了简单网络，那多层多神经元的深度网络呢？

事实上基本一致，第l层网络的梯度为：

$\delta^l = \Sigma'(z^l) (w^{l+1})^T \Sigma'(z^{l+1}) (w^{l+2})^T \ldots \Sigma'(z^L) \nabla_a C$

$\Sigma'(z^l)$ 是一个对角矩阵，他的项是加权输入的值 $\sigma'(z)$ 。 $w^l$ 是不同层的weights矩阵。 $\nabla_a C$ 是C对输出激活的偏导向量。

这比原来的简单神经元复杂多了。但是基本形式还是相似的，很多项 $(w^j)^T \Sigma'(z^j)$ ， $\Sigma'(z^l)$ 对角上的值也不会大于1*4,。只要 $w^j$ 不是太大， $(w^j)^T \Sigma'(z^l)$ 会让梯度变小，导致梯度消失。更一般的，乘积项多会出现梯度不稳定，结果就是导致了学习缓慢。这个缓慢不是意外：这是学习中的一个基本情况。