Michael Nielsen对梯度消失的解释(一)
Contact me:
Email -> cugtyt@qq.com
GitHub -> Cugtyt@GitHub
当我们训练深度网络时出了什么问题?
为了回答这个问题,我们先重新看下只有一个隐层的神经网络,还是使用MNIST。
(网络有三层:784,30,10)
网络的输入层有784个神经元,对应于输入图像像素28*28=784。我们使用30个隐层神经元,10个输出神经元,对应于10个数字类别。
让我们训练30个完整周期,使用mini-batches一次训练10个样本,学习率0.1,正规化参数5.0,我们得到96.48的准确率,现在我们增加一个隐层,还是30个神经元,同样的参数训练(四层网络:784,30,30,10),达到96.57准确率,和原来的差不多,假如我们再加入一层(五层网络:784,30,30,30,10),准确率掉到96.53,这不是个明显的掉落,但是也足够让人灰心了。
有点奇怪,直觉上说,加入隐层应该让网络更加复杂,也应该分类的更好,至少新的隐层什么也不做也不应该更差,但其实不是这样。
所以发生了什么?让我们假设新的隐层在原理上的确有所帮助,问题是我们的学习算法没有找到合适的weights和biases。我们想找出其中出了什么问题,怎么变好。
我们看下网络时怎么学的,下面我画出了网络(四层:784,30,30,10)的一部分,图中每个神经元有一个小长条,表示学习有多快。越长表示学习的越快,越短表示越慢。准确来说,长条表示每个神经元的梯度,就是损失函数对biases的改变率。我们知道梯度控制了学习过程中biases和weights改变的快慢。
为了让图简单,我只是用了两个隐层中的上面6个神经元,略去了输入神经元,因为他们没什么weights和biases要学,输出也略去了,因为我们我们要在层之间比较,相同数量的神经元更方便。
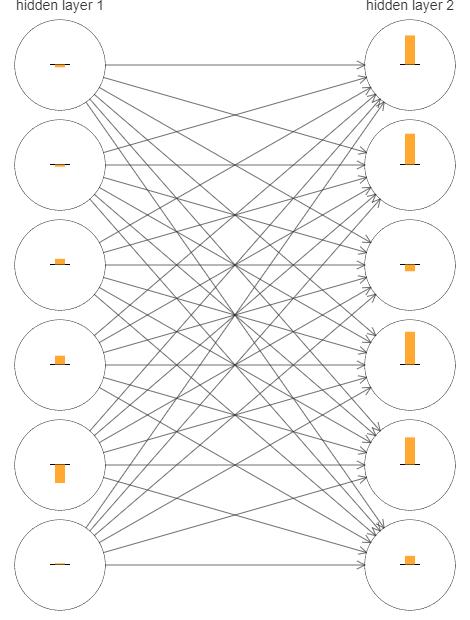
我们使用了随机初始化,但是很明显看到第二个隐层的神经元基本都比第一层的变化快,因此第二隐层的神经元要更快些,这是巧合,还是通常情况?
有个比较两个隐层的整体方法对验证它很有帮助,让我们把第l层第j个神经元的梯度表示为,可以认为
表示第一隐层学习多快,
表示第二隐层学习多块。然后用长度表示每层学习的速度,例如
的长度表示第一隐层的速度,
表示第二隐层的速度。
这些定义下,我们发现,
,所以这验证了:第二隐层比第一隐层学习快得多。
如果我们再加隐层呢?如果有三个隐层(5层:784,30,30,30,10),学习速度为0.012,0.060,0.283,再一次,前面隐层的学习慢于后面的隐层,如果再加一层,那就是0.003,0.017,0.070,0.285,所以说前面隐层学习慢于后面隐层的模式是站得住脚的。
我们已经看了训练开始时学习速度,那训练网络时变化的速度呢?让我们再看两个隐层的网络,学习变化的速度是这样的:
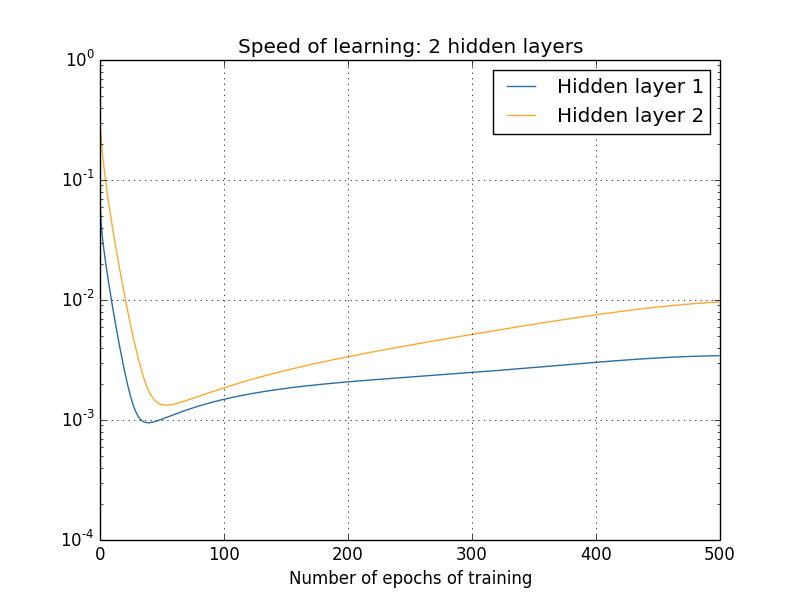
我是用1000个训练图片,批量梯度下降500周期得到这个结果。(略去不重要内容)
你可以看到两层开始于不同的速度,在反弹前下降非常快。但是整体来看,第一隐层比第二隐层慢得多。
更复杂点的网络呢?下面是个相似的情况,使用了三个隐层(784,30,30,30,10):
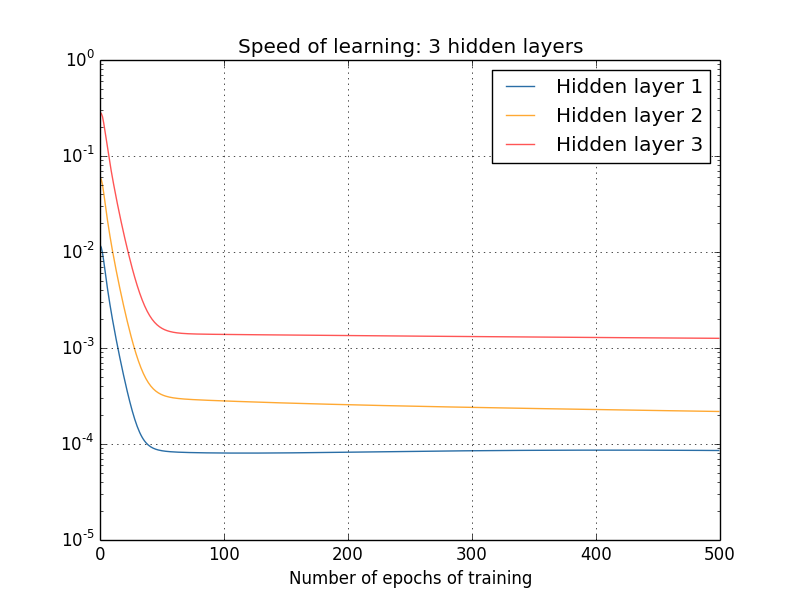
结论是一样的,四层隐层呢?
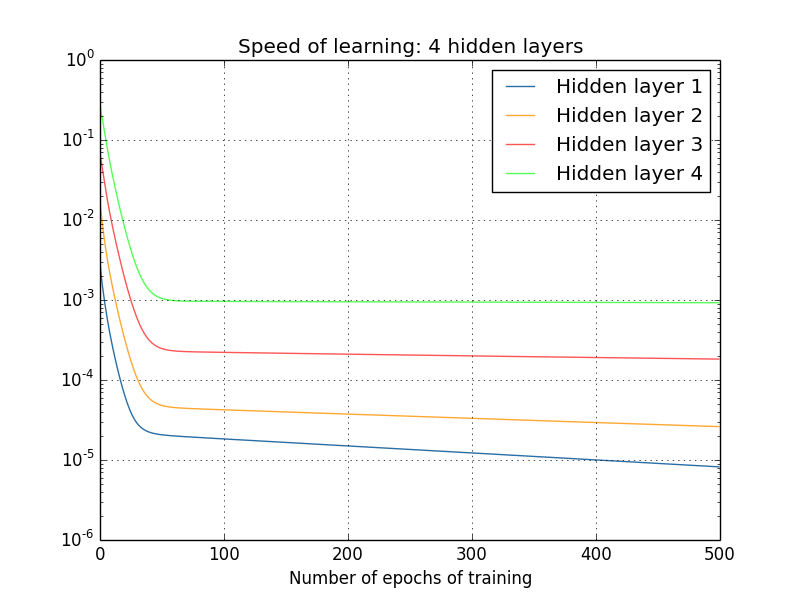
这一次,第一隐层比最后的隐层慢了100倍。不用怀疑我们前面遇到的问题了!
观察到重要的一点:至少一些深度神经网络,梯度在反向上变小。这意味着前面的层比后面的层学习慢的多,我们已经在一个简单的网络上看出来了,这也是很多神经网络遇到的根本问题,这个现象称为梯度消失问题。
为什么梯度消失问题会出现?我们可以避免它吗?在训练深度神经网络时我们怎么解决它?事实上,我们等会儿会说到这是无法避免的,可用的方法也并不吸引人:有时候前面层的梯度会非常大!这称作梯度爆炸问题,并不比梯度消失问题好到哪去。一般来说,深度神经网络的梯度时不稳定的,在前面的层总是倾向于很大或很小。这也是深度神经网络基于梯度算法的根本性问题。
一个对梯度损失的反应是,这对我们来说的确是个问题吗?从神经网络跳出来,想象我们试着用数值方法最小化单变量函数,梯度很小不是个好消息吗?不是意味着我们已经接近了极值点吗?相似的,深度网络前面层梯度小意味着我们不需要对weights和biases做太多调整了吗?
当然并不是这样,回想我们使用随机方法初始化weights和biases,极不可能神经网络已经到达了我们希望的情况。具体而言,考虑网络(五层:784,30,30,30,10)第一层的权重,随机初始化意味着第一层丢弃了大部分输入图像的信息,后面层再怎么训练,他们也很难判别输入图像,因为他们没有足够的信息。故第一层不可能学到太多东西,如果你要训练深度网络,你应该试着去解决它。