Michael Nielsen对交叉熵的解释(二)
Contact me:
Email -> cugtyt@qq.com
GitHub -> Cugtyt@GitHub
- Michael Nielsen对交叉熵的解释(一)
- Michael Nielsen对交叉熵的解释(二)
- Michael Nielsen对交叉熵的解释(三)
我们可以用不同于二次损失函数的损失函数,也就是交叉熵。我们假设使用多个输入变量,相对应的weights为
,bias
:
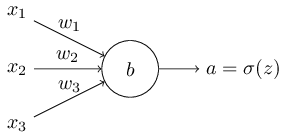
输出是,输入的加权和是
,这个神经元的交叉熵损失函数定义为:
n表示训练数据的总数,x和y是输入和输出。
上面的式子并没有明显表明改善了学习缓慢的问题。事实上,能叫它损失函数都不是很明显!在解决学习缓慢问题之前,我们看下为什么交叉熵为什么可以看做损失函数。
两个属性让它成为损失函数。第一,非负,注意到:(a)求和里面所有项是负的,因为对数里面的数是在0到1之间;(b)求和外面有个负号。第二,如果神经元的输出很接近期望输出,那么交叉熵接近0,例如y=0,a~=0,可以看到由于-ln(1-a)~0,结果接近0,反之对y=1,a~1也一样成立。所以期望输出和实际输出接近时损失函数非常小。
总结起来,交叉熵是正的,当输出结果和期望值接近时趋于0。这是我们期望损失函数具备的属性。当然二次函数也具备这些属性。这对交叉熵是个好消息,但是不同于二次损失函数,交叉熵有一个好处是避免了学习缓慢的问题。让我们计算交叉熵对weights的偏导,得到:
通分之后简化为:
由sigmoid定义,得到导数
。继续简化为:
一个优美的表达式。它告诉我们weight的学习率由控制,也就是说由输出的错误情况决定。错误越大,神经元学习的越快,这也是我们所希望的。尤其是,它避免了二次损失函数中
所导致的学习缓慢。当我们使用交叉熵时,
被约去了,我们不再担心变慢的问题。这真是个奇迹!倒也不是奇迹了,交叉熵正是因为这种属性特殊选择出来的。
类似的方法,我们计算bias的偏导:
再一次,它避免了学习缓慢的问题。